Question Number 126078 by amns last updated on 17/Dec/20
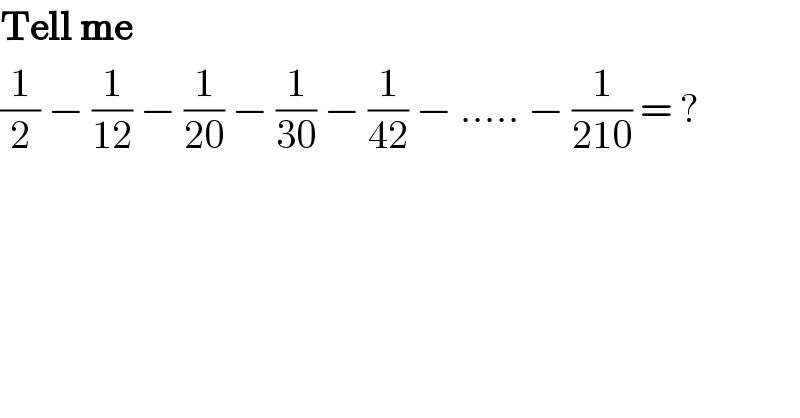
$$\boldsymbol{\mathrm{Tell}}\:\boldsymbol{\mathrm{me}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\mathrm{12}}\:−\:\frac{\mathrm{1}}{\mathrm{20}}\:−\:\frac{\mathrm{1}}{\mathrm{30}}\:−\:\frac{\mathrm{1}}{\mathrm{42}}\:−\:…..\:−\:\frac{\mathrm{1}}{\mathrm{210}}\:=\:? \\ $$
Commented by Dwaipayan Shikari last updated on 17/Dec/20

$$\frac{\mathrm{7}}{\mathrm{30}} \\ $$
Answered by Olaf last updated on 17/Dec/20
![S = (1/2)−Σ_(n=1) ^(12) (1/(n^2 +5n+6)) S = (1/2)−Σ_(n=1) ^(12) (1/((n+2)(n+3))) S = (1/2)−Σ_(n=1) ^(12) [(1/(n+2))−(1/(n+3))] S = (1/2)−[(1/3)−(1/(15))] S = (1/2)−(4/(15)) = (7/(30))](https://www.tinkutara.com/question/Q126143.png)
$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{2}}−\underset{{n}=\mathrm{1}} {\overset{\mathrm{12}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{5}{n}+\mathrm{6}} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{2}}−\underset{{n}=\mathrm{1}} {\overset{\mathrm{12}} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{2}}−\underset{{n}=\mathrm{1}} {\overset{\mathrm{12}} {\sum}}\left[\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right] \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{2}}−\left[\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{15}}\right] \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{15}}\:=\:\frac{\mathrm{7}}{\mathrm{30}} \\ $$
