Question Number 47510 by Rio Michael last updated on 11/Nov/18
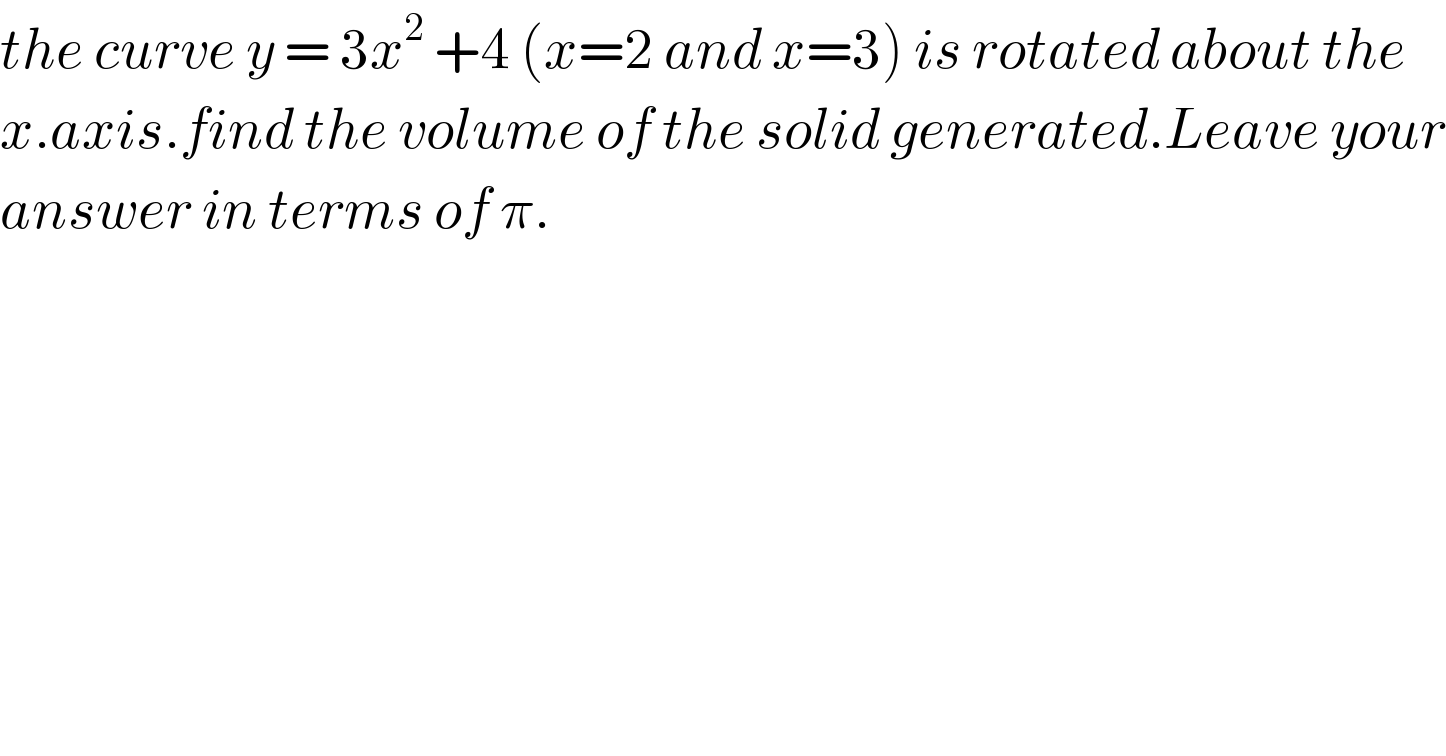
$${the}\:{curve}\:{y}\:=\:\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{4}\:\left({x}=\mathrm{2}\:{and}\:{x}=\mathrm{3}\right)\:{is}\:{rotated}\:{about}\:{the}\: \\ $$$${x}.{axis}.{find}\:{the}\:{volume}\:{of}\:{the}\:{solid}\:{generated}.{Leave}\:{your} \\ $$$${answer}\:{in}\:{terms}\:{of}\:\pi. \\ $$
Commented by mr W last updated on 11/Nov/18
![V=∫_(x1) ^(x2) 2πx×y×dx=2π∫_2 ^3 (3x^3 +4x)dx =2π[((3x^4 )/4)+2x^2 ]_2 ^3 =2π[((3(3^4 −2^4 ))/4)+2(3^2 −2^2 )] =((235π)/2)](https://www.tinkutara.com/question/Q47512.png)
$${V}=\int_{{x}\mathrm{1}} ^{{x}\mathrm{2}} \mathrm{2}\pi{x}×{y}×{dx}=\mathrm{2}\pi\int_{\mathrm{2}} ^{\mathrm{3}} \left(\mathrm{3}{x}^{\mathrm{3}} +\mathrm{4}{x}\right){dx} \\ $$$$=\mathrm{2}\pi\left[\frac{\mathrm{3}{x}^{\mathrm{4}} }{\mathrm{4}}+\mathrm{2}{x}^{\mathrm{2}} \right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\mathrm{2}\pi\left[\frac{\mathrm{3}\left(\mathrm{3}^{\mathrm{4}} −\mathrm{2}^{\mathrm{4}} \right)}{\mathrm{4}}+\mathrm{2}\left(\mathrm{3}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} \right)\right] \\ $$$$=\frac{\mathrm{235}\pi}{\mathrm{2}} \\ $$
