There-are-two-parallel-planes-each-inclined-to-the-horizontal-at-an-angle-A-particle-is-projected-from-a-point-mid-way-between-the-foot-of-the-two-planes-so-that-it-grazes-one-of-the-planes-and-st

Question Number 18271 by Tinkutara last updated on 01/Aug/17

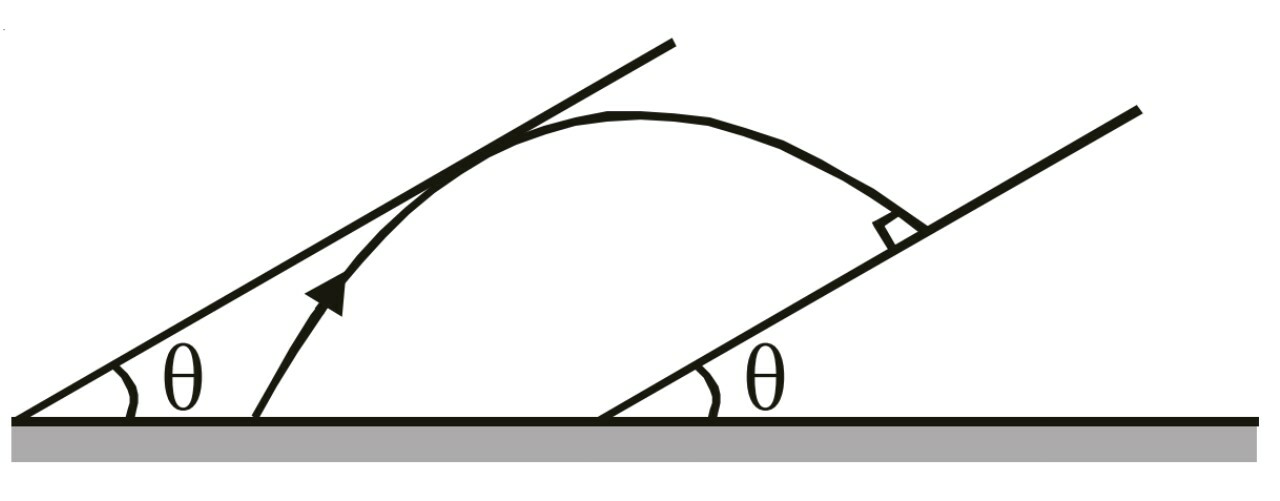
$$\mathrm{There}\:\mathrm{are}\:\mathrm{two}\:\mathrm{parallel}\:\mathrm{planes},\:\mathrm{each} \\ $$$$\mathrm{inclined}\:\mathrm{to}\:\mathrm{the}\:\mathrm{horizontal}\:\mathrm{at}\:\mathrm{an}\:\mathrm{angle}\:\theta. \\ $$$$\mathrm{A}\:\mathrm{particle}\:\mathrm{is}\:\mathrm{projected}\:\mathrm{from}\:\mathrm{a}\:\mathrm{point}\:\mathrm{mid} \\ $$$$\mathrm{way}\:\mathrm{between}\:\mathrm{the}\:\mathrm{foot}\:\mathrm{of}\:\mathrm{the}\:\mathrm{two}\:\mathrm{planes} \\ $$$$\mathrm{so}\:\mathrm{that}\:\mathrm{it}\:\mathrm{grazes}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{planes}\:\mathrm{and} \\ $$$$\mathrm{strikes}\:\mathrm{the}\:\mathrm{other}\:\mathrm{at}\:\mathrm{right}\:\mathrm{angle}.\:\mathrm{Find} \\ $$$$\mathrm{the}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{projection}\:\mathrm{of}\:\mathrm{the}\:\mathrm{projectile}. \\ $$

Commented by Tinkutara last updated on 17/Jul/17

Commented by Tinkutara last updated on 01/Aug/17

$$\mathrm{The}\:\mathrm{point}\:\mathrm{is}\:\mathrm{midpoint}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:\mathrm{joining} \\ $$$$\mathrm{feet}\:\mathrm{of}\:\mathrm{the}\:\mathrm{two}\:\mathrm{planes}\:\left(\mathrm{as}\:\mathrm{not}\:\mathrm{shown}\:\mathrm{in}\right. \\ $$$$\left.\mathrm{the}\:\mathrm{figure}\right). \\ $$

Commented by ajfour last updated on 03/Aug/17

$$\mathrm{I}\:\mathrm{have}\:\mathrm{a}\:\mathrm{method}\:\mathrm{but}\:\mathrm{that}\:\mathrm{fetches} \\ $$$$\mathrm{correct}\:\:\mathrm{answer}\:\mathrm{but}\:\mathrm{in}\:\mathrm{another}\:\mathrm{form}. \\ $$$$\phi=\mathrm{tan}^{−\mathrm{1}} \left[\mathrm{tan}\:\theta+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{tan}\:\theta+\mathrm{cot}\:\theta\right)\right]. \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com