Question Number 174193 by Best1 last updated on 26/Jul/22
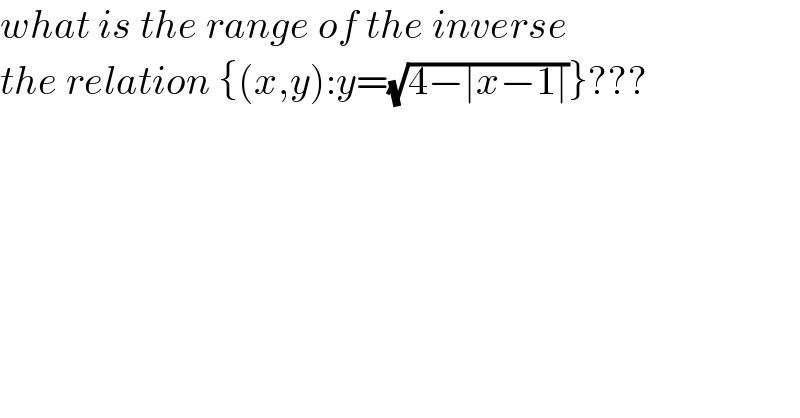
$${what}\:{is}\:{the}\:{range}\:{of}\:{the}\:{inverse}\: \\ $$$${the}\:{relation}\:\left\{\left({x},{y}\right):{y}=\sqrt{\mathrm{4}−\mid{x}−\mathrm{1}\mid}\right\}??? \\ $$
Commented by cortano1 last updated on 27/Jul/22
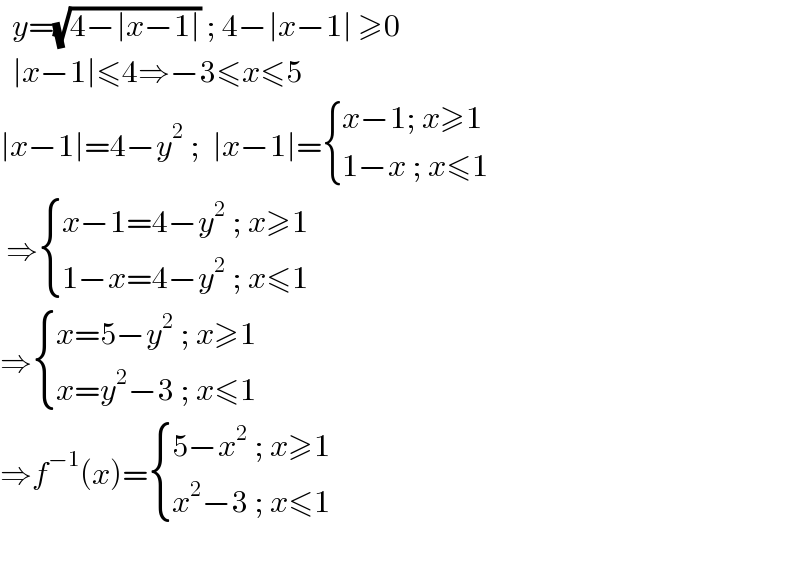
$$\:\:{y}=\sqrt{\mathrm{4}−\mid{x}−\mathrm{1}\mid}\:;\:\mathrm{4}−\mid{x}−\mathrm{1}\mid\:\geqslant\mathrm{0} \\ $$$$\:\:\mid{x}−\mathrm{1}\mid\leqslant\mathrm{4}\Rightarrow−\mathrm{3}\leqslant{x}\leqslant\mathrm{5} \\ $$$$\mid{x}−\mathrm{1}\mid=\mathrm{4}−{y}^{\mathrm{2}} \:;\:\:\mid{x}−\mathrm{1}\mid=\begin{cases}{{x}−\mathrm{1};\:{x}\geqslant\mathrm{1}}\\{\mathrm{1}−{x}\:;\:{x}\leqslant\mathrm{1}}\end{cases} \\ $$$$\:\Rightarrow\begin{cases}{{x}−\mathrm{1}=\mathrm{4}−{y}^{\mathrm{2}} \:;\:{x}\geqslant\mathrm{1}}\\{\mathrm{1}−{x}=\mathrm{4}−{y}^{\mathrm{2}} \:;\:{x}\leqslant\mathrm{1}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{{x}=\mathrm{5}−{y}^{\mathrm{2}} \:;\:{x}\geqslant\mathrm{1}}\\{{x}={y}^{\mathrm{2}} −\mathrm{3}\:;\:{x}\leqslant\mathrm{1}}\end{cases} \\ $$$$\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\begin{cases}{\mathrm{5}−{x}^{\mathrm{2}} \:;\:{x}\geqslant\mathrm{1}}\\{{x}^{\mathrm{2}} −\mathrm{3}\:;\:{x}\leqslant\mathrm{1}}\end{cases} \\ $$$$\: \\ $$
Commented by kaivan.ahmadi last updated on 27/Jul/22
![R_f^(−1) =D_f 4−∣x−1∣≥0⇒∣x−1∣≤4⇒ −4≤x−1≤4⇒−3≤x≤5 ⇒R_f^(−1) =[−3,5]](https://www.tinkutara.com/question/Q174247.png)
$${R}_{{f}^{−\mathrm{1}} } ={D}_{{f}} \\ $$$$\mathrm{4}−\mid{x}−\mathrm{1}\mid\geqslant\mathrm{0}\Rightarrow\mid{x}−\mathrm{1}\mid\leqslant\mathrm{4}\Rightarrow \\ $$$$−\mathrm{4}\leqslant{x}−\mathrm{1}\leqslant\mathrm{4}\Rightarrow−\mathrm{3}\leqslant{x}\leqslant\mathrm{5} \\ $$$$\Rightarrow{R}_{{f}^{−\mathrm{1}} } =\left[−\mathrm{3},\mathrm{5}\right] \\ $$
