Question Number 174439 by mnjuly1970 last updated on 01/Aug/22
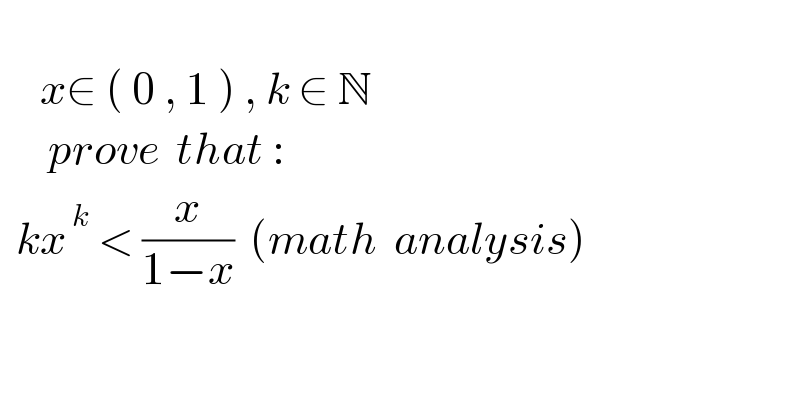
$$ \\ $$$$\:\:\:\:\:{x}\in\:\left(\:\mathrm{0}\:,\:\mathrm{1}\:\right)\:,\:{k}\:\in\:\mathbb{N} \\ $$$$\:\:\:\:\:\:{prove}\:\:{that}\:: \\ $$$$\:\:{kx}^{\:{k}} \:<\:\frac{{x}}{\mathrm{1}−{x}}\:\:\left({math}\:\:{analysis}\right) \\ $$$$ \\ $$
Answered by behi834171 last updated on 01/Aug/22
![for: k=1: 1×x^1 <^? (x/(1−x))⇒x<^? (x/(1−x)) 0<x<1⇒−1<−x<0⇒0<1−x<1 so: 1−x<1⇒(x/(1−x))>x , i.e:it is true for : k=1 let assume that is true for k=n we should prove that is true for k=n+1 (n+1)x^(n+1) <^? (x/(1−x)) (n+1)x^(n+1) (1−x)=(n+1)x^(n+1) −(n+1)x^(n+2) < <nx^n .x+x^(n+1) −nx^n .x^2 −x^(n+2) <(x/(1−x)).x−(x/(1−x)).x^2 +x^(n+1) −x^(n+2) = =((x^2 −x^3 )/(1−x))+x^(n+1) −x^(n+2) =x^2 +x^(n+1) −x^(n+2) < <x+x−x=x .hence proved. ■ [0<x<1⇒ x^(p∈N) <x]](https://www.tinkutara.com/question/Q174448.png)
$${for}:\:\:{k}=\mathrm{1}:\:\:\mathrm{1}×{x}^{\mathrm{1}} \overset{?} {<}\frac{{x}}{\mathrm{1}−{x}}\Rightarrow{x}\overset{?} {<}\frac{{x}}{\mathrm{1}−{x}} \\ $$$$\mathrm{0}<{x}<\mathrm{1}\Rightarrow−\mathrm{1}<−{x}<\mathrm{0}\Rightarrow\mathrm{0}<\mathrm{1}−{x}<\mathrm{1} \\ $$$${so}:\:\mathrm{1}−{x}<\mathrm{1}\Rightarrow\frac{{x}}{\mathrm{1}−{x}}>{x}\:, \\ $$$${i}.{e}:{it}\:{is}\:{true}\:{for}\::\:{k}=\mathrm{1} \\ $$$${let}\:{assume}\:{that}\:{is}\:{true}\:{for}\:{k}={n} \\ $$$${we}\:{should}\:{prove}\:{that}\:{is}\:{true}\:{for}\:{k}={n}+\mathrm{1} \\ $$$$\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} \overset{?} {<}\frac{{x}}{\mathrm{1}−{x}} \\ $$$$\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} \left(\mathrm{1}−{x}\right)=\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{2}} < \\ $$$$<{nx}^{{n}} .{x}+{x}^{{n}+\mathrm{1}} −{nx}^{{n}} .{x}^{\mathrm{2}} −{x}^{{n}+\mathrm{2}} \\ $$$$<\frac{{x}}{\mathrm{1}−{x}}.{x}−\frac{{x}}{\mathrm{1}−{x}}.{x}^{\mathrm{2}} +{x}^{{n}+\mathrm{1}} −{x}^{{n}+\mathrm{2}} = \\ $$$$=\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{3}} }{\mathrm{1}−{x}}+{x}^{{n}+\mathrm{1}} −{x}^{{n}+\mathrm{2}} ={x}^{\mathrm{2}} +{x}^{{n}+\mathrm{1}} −{x}^{{n}+\mathrm{2}} < \\ $$$$<{x}+{x}−{x}=\boldsymbol{{x}}\:\:.\boldsymbol{{hence}}\:\boldsymbol{{proved}}.\:\blacksquare \\ $$$$\left[\mathrm{0}<\boldsymbol{{x}}<\mathrm{1}\Rightarrow\:\:\:\boldsymbol{{x}}^{\boldsymbol{{p}}\in\boldsymbol{{N}}} <\boldsymbol{{x}}\right] \\ $$
