Question Number 16589 by ajfour last updated on 24/Jun/17
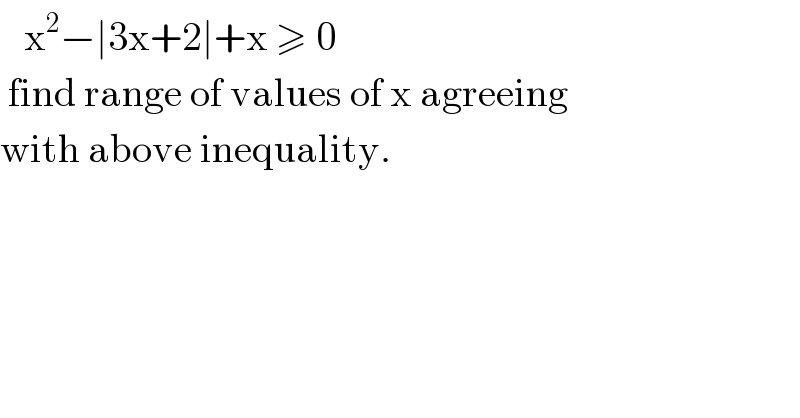
$$\:\:\:\mathrm{x}^{\mathrm{2}} −\mid\mathrm{3x}+\mathrm{2}\mid+\mathrm{x}\:\geqslant\:\mathrm{0} \\ $$$$\:\mathrm{find}\:\mathrm{range}\:\mathrm{of}\:\mathrm{values}\:\mathrm{of}\:\mathrm{x}\:\mathrm{agreeing} \\ $$$$\mathrm{with}\:\mathrm{above}\:\mathrm{inequality}. \\ $$
Answered by mrW1 last updated on 24/Jun/17
![if 3x+2≥0 or x≥−(2/3) (≈−0.67) x^2 −3x−2+x≥0 x^2 −2x+1−3≥0 (x−1)^2 ≥3 x−1≥(√3) ⇒x≥1+(√3) or x−1≤−(√3) ⇒x≤1−(√3) (≈−0.73) ≱−(2/3) ⇒⇒x≥1+(√3) if 3x+2<0 or x<−(2/3) (≈−0.67) x^2 +3x+2+x≥0 x^2 +4x+2≥0 (x+2)^2 ≥2 x+2≥(√2) ⇒x≥−2+(√2) (≈−0.59) ≮−(2/3) or x+2≤−(√2) ⇒x≤−2−(√2) (≈−3.41) ⇒⇒x≤−2−(√2) ⇒x∈(−∞,−2−(√2) ] ∧ [1+(√3),+∞)](https://www.tinkutara.com/question/Q16590.png)
$$\mathrm{if}\:\mathrm{3x}+\mathrm{2}\geqslant\mathrm{0}\:\mathrm{or}\:\mathrm{x}\geqslant−\frac{\mathrm{2}}{\mathrm{3}}\:\left(\approx−\mathrm{0}.\mathrm{67}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{2}+\mathrm{x}\geqslant\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}−\mathrm{3}\geqslant\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \geqslant\mathrm{3} \\ $$$$\mathrm{x}−\mathrm{1}\geqslant\sqrt{\mathrm{3}}\:\Rightarrow\mathrm{x}\geqslant\mathrm{1}+\sqrt{\mathrm{3}} \\ $$$$\mathrm{or} \\ $$$$\mathrm{x}−\mathrm{1}\leqslant−\sqrt{\mathrm{3}}\:\Rightarrow\mathrm{x}\leqslant\mathrm{1}−\sqrt{\mathrm{3}}\:\:\left(\approx−\mathrm{0}.\mathrm{73}\right)\:\ngeq−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\Rightarrow\mathrm{x}\geqslant\mathrm{1}+\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{3x}+\mathrm{2}<\mathrm{0}\:\mathrm{or}\:\mathrm{x}<−\frac{\mathrm{2}}{\mathrm{3}}\:\left(\approx−\mathrm{0}.\mathrm{67}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{2}+\mathrm{x}\geqslant\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{2}\geqslant\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \geqslant\mathrm{2} \\ $$$$\mathrm{x}+\mathrm{2}\geqslant\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{x}\geqslant−\mathrm{2}+\sqrt{\mathrm{2}}\:\:\left(\approx−\mathrm{0}.\mathrm{59}\right)\:\nless−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{or} \\ $$$$\mathrm{x}+\mathrm{2}\leqslant−\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{x}\leqslant−\mathrm{2}−\sqrt{\mathrm{2}}\:\:\left(\approx−\mathrm{3}.\mathrm{41}\right) \\ $$$$\Rightarrow\Rightarrow\mathrm{x}\leqslant−\mathrm{2}−\sqrt{\mathrm{2}}\: \\ $$$$ \\ $$$$\Rightarrow\mathrm{x}\in\left(−\infty,−\mathrm{2}−\sqrt{\mathrm{2}}\:\right]\:\wedge\:\left[\mathrm{1}+\sqrt{\mathrm{3}},+\infty\right) \\ $$
Commented by ajfour last updated on 24/Jun/17
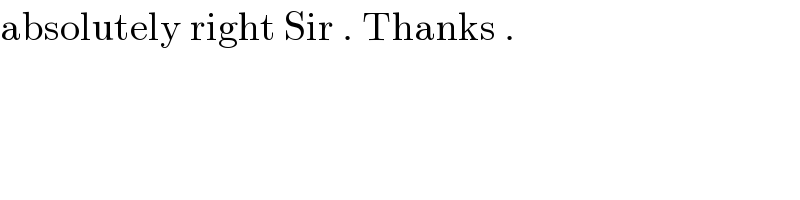
$$\mathrm{absolutely}\:\mathrm{right}\:\mathrm{Sir}\:.\:\mathrm{Thanks}\:. \\ $$
