Question Number 185734 by Shrinava last updated on 26/Jan/23
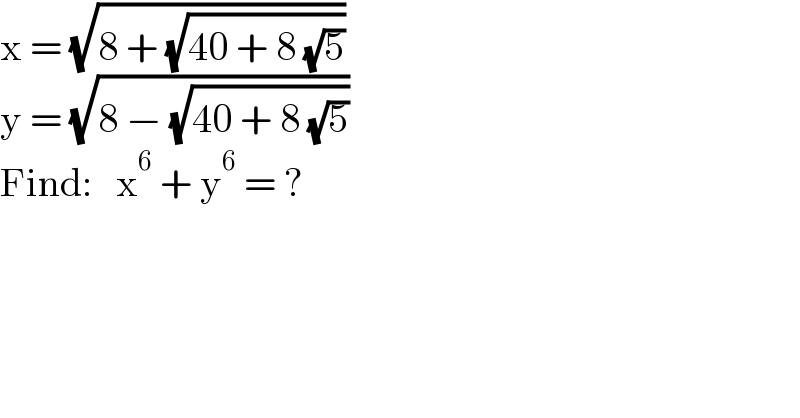
$$\mathrm{x}\:=\:\sqrt{\mathrm{8}\:+\:\sqrt{\mathrm{40}\:+\:\mathrm{8}\:\sqrt{\mathrm{5}}}} \\ $$$$\mathrm{y}\:=\:\sqrt{\mathrm{8}\:−\:\sqrt{\mathrm{40}\:+\:\mathrm{8}\:\sqrt{\mathrm{5}}}} \\ $$$$\mathrm{Find}:\:\:\:\mathrm{x}^{\mathrm{6}} \:+\:\mathrm{y}^{\mathrm{6}} \:=\:? \\ $$
Answered by abdullarasool last updated on 26/Jan/23

$$ \\ $$
Answered by HeferH last updated on 26/Jan/23
![a = 8 b = (√(40+8(√5))) ⇒ x = (√(a + b)) y = (√(a − b)) (x^2 )^3 +(y^2 )^3 = (x^2 +y^2 )(x^4 +y^4 − x^2 y^2 ) = 2a[(a+b)^2 + (a − b)^2 − (a−b)(a+b)] = 2a[2a^2 +2b^2 −a^2 + b^2 ] = 2a(a^2 +3b^2 ) = 2a^3 +6b^2 a ⇒ 2(8^3 )+ 6∙((√(40+8(√5))))^2 8 = 1024 + 48(40 + 8(√5)) = 1024 + 1920 + 384(√5) = 2944 + 384(√5)](https://www.tinkutara.com/question/Q185738.png)
$$\:{a}\:=\:\mathrm{8} \\ $$$$\:{b}\:=\:\sqrt{\mathrm{40}+\mathrm{8}\sqrt{\mathrm{5}}}\:\Rightarrow \\ $$$$\:{x}\:=\:\sqrt{{a}\:+\:{b}} \\ $$$$\:{y}\:=\:\sqrt{{a}\:−\:{b}} \\ $$$$\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} +\left({y}^{\mathrm{2}} \right)^{\mathrm{3}} \:=\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{4}} +{y}^{\mathrm{4}} \:−\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)\:\: \\ $$$$=\:\mathrm{2}{a}\left[\left({a}+{b}\right)^{\mathrm{2}} \:+\:\left({a}\:−\:{b}\right)^{\mathrm{2}} \:−\:\left({a}−{b}\right)\left({a}+{b}\right)\right]\: \\ $$$$=\:\mathrm{2}{a}\left[\mathrm{2}{a}^{\mathrm{2}} \:+\mathrm{2}{b}^{\mathrm{2}} \:−{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \right]\: \\ $$$$=\:\mathrm{2}{a}\left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \right)\:=\:\:\mathrm{2}{a}^{\mathrm{3}} +\mathrm{6}{b}^{\mathrm{2}} {a} \\ $$$$\:\:\Rightarrow \\ $$$$\:\mathrm{2}\left(\mathrm{8}^{\mathrm{3}} \right)+\:\mathrm{6}\centerdot\left(\sqrt{\mathrm{40}+\mathrm{8}\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} \mathrm{8}\: \\ $$$$=\:\mathrm{1024}\:+\:\mathrm{48}\left(\mathrm{40}\:+\:\mathrm{8}\sqrt{\mathrm{5}}\right) \\ $$$$=\:\mathrm{1024}\:+\:\mathrm{1920}\:+\:\mathrm{384}\sqrt{\mathrm{5}}\: \\ $$$$=\:\mathrm{2944}\:+\:\mathrm{384}\sqrt{\mathrm{5}}\: \\ $$
Answered by mr W last updated on 26/Jan/23
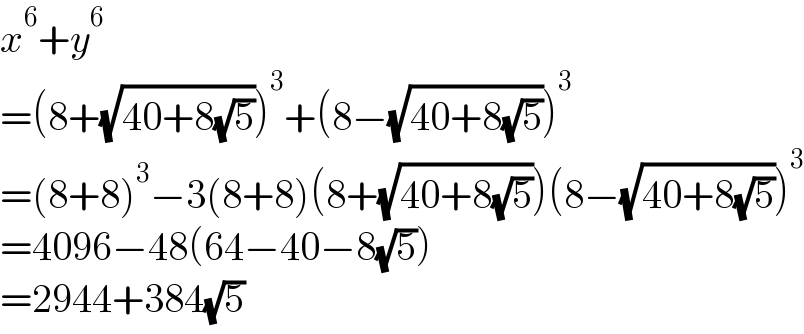
$${x}^{\mathrm{6}} +{y}^{\mathrm{6}} \\ $$$$=\left(\mathrm{8}+\sqrt{\mathrm{40}+\mathrm{8}\sqrt{\mathrm{5}}}\right)^{\mathrm{3}} +\left(\mathrm{8}−\sqrt{\mathrm{40}+\mathrm{8}\sqrt{\mathrm{5}}}\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{8}+\mathrm{8}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{8}+\mathrm{8}\right)\left(\mathrm{8}+\sqrt{\mathrm{40}+\mathrm{8}\sqrt{\mathrm{5}}}\right)\left(\mathrm{8}−\sqrt{\mathrm{40}+\mathrm{8}\sqrt{\mathrm{5}}}\right)^{\mathrm{3}} \\ $$$$=\mathrm{4096}−\mathrm{48}\left(\mathrm{64}−\mathrm{40}−\mathrm{8}\sqrt{\mathrm{5}}\right) \\ $$$$=\mathrm{2944}+\mathrm{384}\sqrt{\mathrm{5}} \\ $$
Answered by manxsol last updated on 27/Jan/23
![x=(√(a+(√b))) y=(√(a−(√b))) x^6 +y^6 =(x^2 )^3 +(y^2 )^3 = [(a+(√b))+(a−(√b))[(a+(√b))^2 − (a+(√b))(a−(√b))+(a−(√b))^2 ]= 2a[2(a^2 +b)−(a^2 −b)]= 2a[a^2 +3b] reemplazando a=8 b=40+8(√5) 2944+384(√5)](https://www.tinkutara.com/question/Q185763.png)
$${x}=\sqrt{{a}+\sqrt{{b}}} \\ $$$${y}=\sqrt{{a}−\sqrt{{b}}} \\ $$$${x}^{\mathrm{6}} +{y}^{\mathrm{6}} =\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} +\left({y}^{\mathrm{2}} \right)^{\mathrm{3}} = \\ $$$$\left[\left({a}+\sqrt{{b}}\right)+\left({a}−\sqrt{{b}}\right)\left[\left({a}+\sqrt{{b}}\right)^{\mathrm{2}} −\right.\right. \\ $$$$\left.\left({a}+\sqrt{{b}}\right)\left({a}−\sqrt{{b}}\right)+\left({a}−\sqrt{{b}}\right)^{\mathrm{2}} \right]= \\ $$$$\mathrm{2}{a}\left[\mathrm{2}\left({a}^{\mathrm{2}} +{b}\right)−\left({a}^{\mathrm{2}} −{b}\right)\right]= \\ $$$$\mathrm{2}{a}\left[{a}^{\mathrm{2}} +\mathrm{3}{b}\right] \\ $$$${reemplazando} \\ $$$${a}=\mathrm{8} \\ $$$${b}=\mathrm{40}+\mathrm{8}\sqrt{\mathrm{5}} \\ $$$$\mathrm{2944}+\mathrm{384}\sqrt{\mathrm{5}} \\ $$
Commented by Shrinava last updated on 28/Jan/23
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professors} \\ $$
