Question Number 89973 by john santu last updated on 20/Apr/20
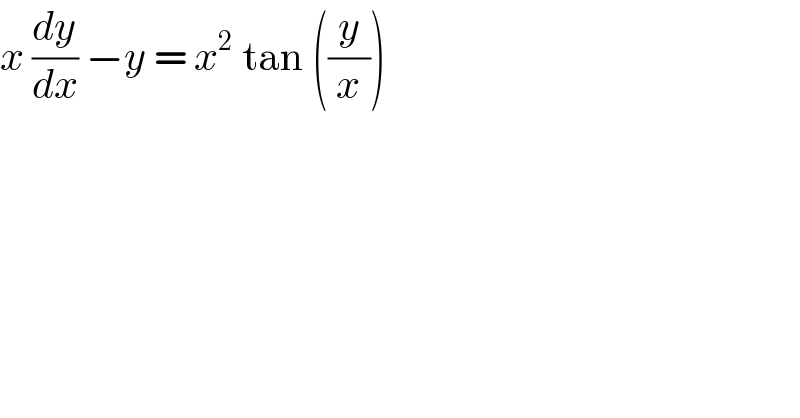
$${x}\:\frac{{dy}}{{dx}}\:−{y}\:=\:{x}^{\mathrm{2}} \:\mathrm{tan}\:\left(\frac{{y}}{{x}}\right)\: \\ $$
Commented by john santu last updated on 20/Apr/20
![[ let (y/x)= v ⇒y = vx ] (dy/dx) = v + x (dv/dx) x [ v+x (dv/dx) ]−vx = x^2 tan v v + x (dv/dx) −v = x tan v x (dv/dx) = x tan v ⇒ (dv/(tan v)) = dx ∫ ((cos v dv)/(sin v)) = ∫ dx ∫ ((d(sin v))/(sin v)) = x +c ln ∣sin v∣ = x+c sin v = ± C e^x sin ((y/x)) = ±Ce^x](https://www.tinkutara.com/question/Q89976.png)
$$\left[\:{let}\:\frac{{y}}{{x}}=\:{v}\:\Rightarrow{y}\:=\:{vx}\:\right]\: \\ $$$$\frac{{dy}}{{dx}}\:=\:{v}\:+\:{x}\:\frac{{dv}}{{dx}} \\ $$$${x}\:\left[\:{v}+{x}\:\frac{{dv}}{{dx}}\:\right]−{vx}\:=\:{x}^{\mathrm{2}} \:\mathrm{tan}\:{v}\: \\ $$$${v}\:+\:{x}\:\frac{{dv}}{{dx}}\:−{v}\:=\:{x}\:\mathrm{tan}\:{v}\: \\ $$$${x}\:\frac{{dv}}{{dx}}\:=\:{x}\:\mathrm{tan}\:{v}\:\Rightarrow\:\frac{{dv}}{\mathrm{tan}\:{v}}\:=\:{dx} \\ $$$$\int\:\frac{\mathrm{cos}\:{v}\:{dv}}{\mathrm{sin}\:{v}}\:=\:\int\:{dx}\: \\ $$$$\int\:\frac{{d}\left(\mathrm{sin}\:{v}\right)}{\mathrm{sin}\:{v}}\:=\:{x}\:+{c}\: \\ $$$$\mathrm{ln}\:\mid\mathrm{sin}\:{v}\mid\:=\:{x}+{c}\: \\ $$$$\mathrm{sin}\:{v}\:=\:\pm\:{C}\:{e}^{{x}} \\ $$$$\mathrm{sin}\:\left(\frac{{y}}{{x}}\right)\:=\:\pm{Ce}^{{x}} \\ $$
Answered by TANMAY PANACEA. last updated on 20/Apr/20
![((xdy−ydx)/x^2 ).((cos((y/x)))/(sin((y/x))))=dx ∫((cos((y/x))d((y/x)))/(sin((y/x))))=∫dx ln[sin((y/x))]=x+c](https://www.tinkutara.com/question/Q89981.png)
$$\frac{{xdy}−{ydx}}{{x}^{\mathrm{2}} }.\frac{{cos}\left(\frac{{y}}{{x}}\right)}{{sin}\left(\frac{{y}}{{x}}\right)}={dx} \\ $$$$\int\frac{{cos}\left(\frac{{y}}{{x}}\right){d}\left(\frac{{y}}{{x}}\right)}{{sin}\left(\frac{{y}}{{x}}\right)}=\int{dx} \\ $$$${ln}\left[{sin}\left(\frac{{y}}{{x}}\right)\right]={x}+{c} \\ $$
