Question Number 61874 by aliesam last updated on 10/Jun/19
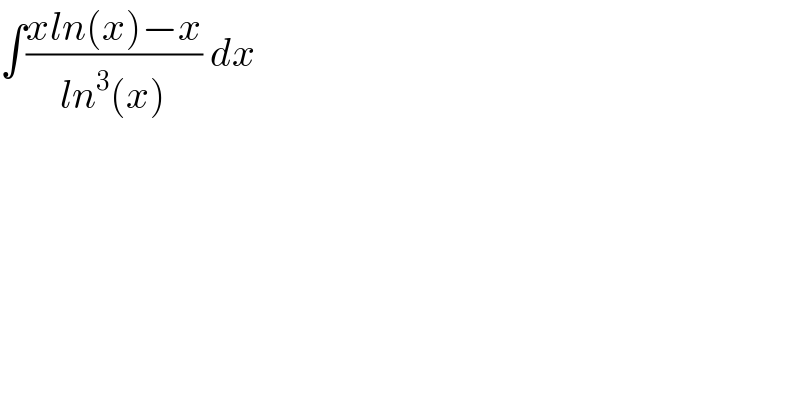
$$\int\frac{{xln}\left({x}\right)−{x}}{{ln}^{\mathrm{3}} \left({x}\right)}\:{dx} \\ $$
Commented by Prithwish sen last updated on 10/Jun/19
![∫[(x/([ln(x)]^2 )) −(x/([ln(x)]^3 )) ]dx applying by parts =(x^2 /(2[ln(x)]^2 )) +∫(x/([ln(x)]^3 )) dx −∫(x/([ln(x)]^(3 ) )) +C =(x^2 /(2[ln(x)]^2 )) +C](https://www.tinkutara.com/question/Q61883.png)
$$\int\left[\frac{\mathrm{x}}{\left[\mathrm{ln}\left(\mathrm{x}\right)\right]^{\mathrm{2}} }\:−\frac{\mathrm{x}}{\left[\mathrm{ln}\left(\mathrm{x}\right)\right]^{\mathrm{3}} }\:\right]\mathrm{dx} \\ $$$$\mathrm{applying}\:\mathrm{by}\:\mathrm{parts} \\ $$$$=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}\left[\mathrm{ln}\left(\mathrm{x}\right)\right]^{\mathrm{2}} }\:+\int\frac{\mathrm{x}}{\left[\mathrm{ln}\left(\mathrm{x}\right)\right]^{\mathrm{3}} }\:\mathrm{dx}\:−\int\frac{\mathrm{x}}{\left[\mathrm{ln}\left(\mathrm{x}\right)\right]^{\mathrm{3}\:} }\:+\mathrm{C} \\ $$$$=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}\left[\mathrm{ln}\left(\mathrm{x}\right)\right]^{\mathrm{2}} }\:+\mathrm{C} \\ $$
