Menu Close

0-1-1-x-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 54033 by qw last updated on 28/Jan/19
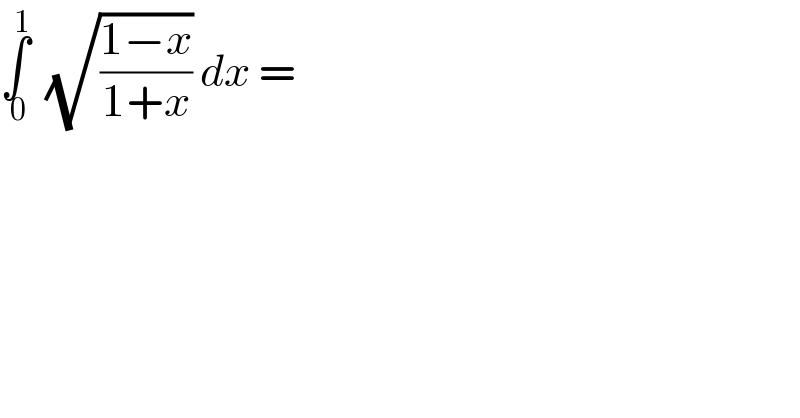
∫_( 0) ^1 (√((1−x)/(1+x))) dx =
$$\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:{dx}\:= \\ $$
Commented by maxmathsup by imad last updated on 29/Jan/19
let I =∫_0 ^1 (√((1−x)/(1+x)))dx let use the chan. (√((1−x)/(1+x)))=t ⇒((1−x)/(1+x)) =t^2 ⇒ 1−x =t^2 +t^2 x ⇒1−t^2 =(1+t^2 )x ⇒x =((1−t^2 )/(1+t^2 )) ⇒ (dx/dt) =((−2t(1+t^2 )−(1−t^2 )(2t))/((1+t^2 )^2 )) =((−2t−2t^3 −2t +2t^3 )/((1+t^2 )^2 )) =((−4t)/((1+t^2 )^2 )) ⇒ I = −∫_0 ^1 t(((−4t)/((1+t^2 )^2 )) )dt =4 ∫_0 ^1 (t^2 /((1+t^2 )^2 )) dt =4{ ∫_0 ^1 ((1+t^2 −1)/((1+t^2 )^2 ))dt}=4{∫_0 ^1 (dt/(1+t^2 )) −∫_0 ^1 (dt/((1+t^2 )^2 ))} but ∫_0 ^1 (dt/(1+t^2 )) =[arctant]_0 ^1 =(π/4) ∫_0 ^1 (dt/((1+t^2 )^2 )) =_(t =tanθ) ∫_0 ^(π/4) (((1+tan^2 θ))/((1+tan^2 θ)^2 ))dθ = ∫_0 ^(π/4) (dθ/(1+tan^2 θ)) =∫_0 ^(π/4) cos^2 θ dθ =∫_0 ^(π/4) ((1+cos(2θ))/2) dθ =(π/8) +(1/4)[sin(2θ)]_0 ^(π/4) =(π/8) +(1/4) ⇒ I =4{(π/4) −(π/8) −(1/4)} =π−(π/2) −1 =(π/2) −1 .
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}{dx}\:\:{let}\:{use}\:{the}\:{chan}.\:\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}={t}\:\Rightarrow\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\:={t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{1}−{x}\:={t}^{\mathrm{2}} \:+{t}^{\mathrm{2}} {x}\:\Rightarrow\mathrm{1}−{t}^{\mathrm{2}} =\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}\:\:\Rightarrow{x}\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:\Rightarrow\:\frac{{dx}}{{dt}}\:=\frac{−\mathrm{2}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)−\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{2}{t}\right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}{t}−\mathrm{2}{t}^{\mathrm{3}} −\mathrm{2}{t}\:+\mathrm{2}{t}^{\mathrm{3}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{−\mathrm{4}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow\:{I}\:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}\left(\frac{−\mathrm{4}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\right){dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dt}\:=\mathrm{4}\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\right\}=\mathrm{4}\left\{\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\right\}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\left[{arctant}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=_{{t}\:={tan}\theta} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }{d}\theta\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{\mathrm{2}} \theta\:{d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\:{d}\theta\:=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left[{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${I}\:=\mathrm{4}\left\{\frac{\pi}{\mathrm{4}}\:−\frac{\pi}{\mathrm{8}}\:−\frac{\mathrm{1}}{\mathrm{4}}\right\}\:=\pi−\frac{\pi}{\mathrm{2}}\:−\mathrm{1}\:=\frac{\pi}{\mathrm{2}}\:−\mathrm{1}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Jan/19
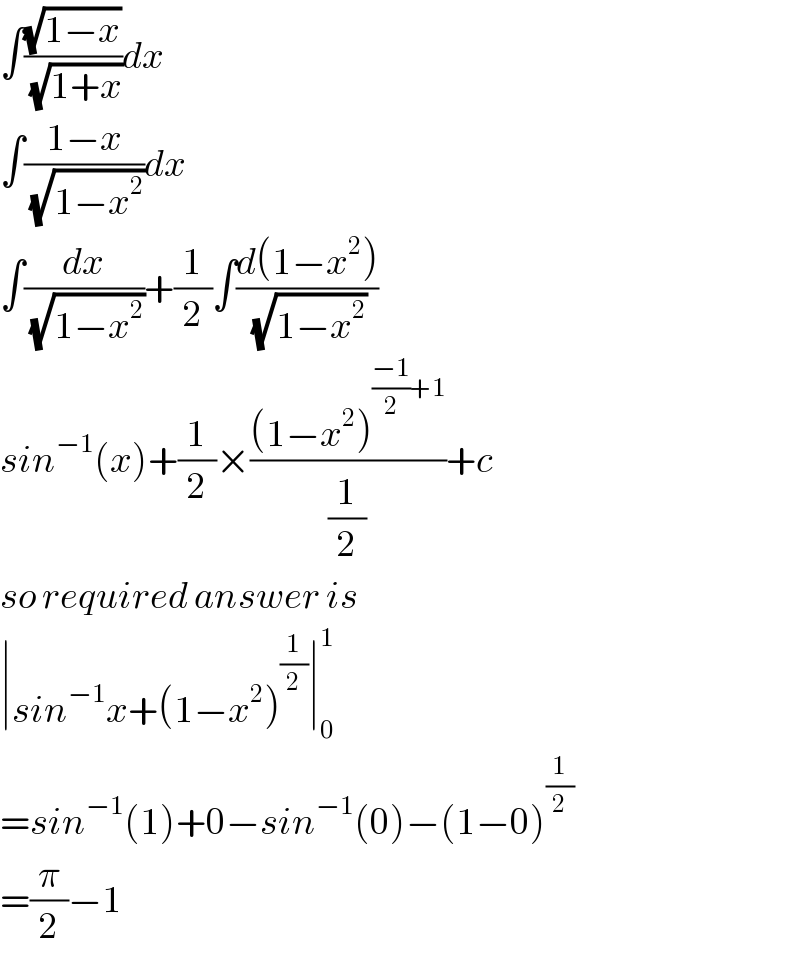
∫((√(1−x))/( (√(1+x))))dx ∫((1−x)/( (√(1−x^2 ))))dx ∫(dx/( (√(1−x^2 ))))+(1/2)∫((d(1−x^2 ))/( (√(1−x^2 )))) sin^(−1) (x)+(1/2)×(((1−x^2 )^(((−1)/2)+1) )/(1/2))+c so required answer is ∣sin^(−1) x+(1−x^2 )^(1/2) ∣_0 ^1 =sin^(−1) (1)+0−sin^(−1) (0)−(1−0)^(1/2) =(π/2)−1
$$\int\frac{\sqrt{\mathrm{1}−{x}}}{\:\sqrt{\mathrm{1}+{x}}}{dx} \\ $$$$\int\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$\int\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${sin}^{−\mathrm{1}} \left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} }{\frac{\mathrm{1}}{\mathrm{2}}}+{c} \\ $$$${so}\:{required}\:{answer}\:{is} \\ $$$$\mid{sin}^{−\mathrm{1}} {x}+\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$={sin}^{−\mathrm{1}} \left(\mathrm{1}\right)+\mathrm{0}−{sin}^{−\mathrm{1}} \left(\mathrm{0}\right)−\left(\mathrm{1}−\mathrm{0}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$
Answered by ajfour last updated on 28/Jan/19
let x=cos 2θ ∫_(π/4) ^( 0) tan θ(−4sin θcos θ)dθ =2∫_0 ^( π/4) (1−cos 2θ)dθ = (π/2)−1 .
$${let}\:{x}=\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\int_{\pi/\mathrm{4}} ^{\:\:\mathrm{0}} \mathrm{tan}\:\theta\left(−\mathrm{4sin}\:\theta\mathrm{cos}\:\theta\right){d}\theta \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right){d}\theta\: \\ $$$$\:=\:\frac{\pi}{\mathrm{2}}−\mathrm{1}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *