Question Number 85846 by Jakir Sarif Mondal last updated on 25/Mar/20
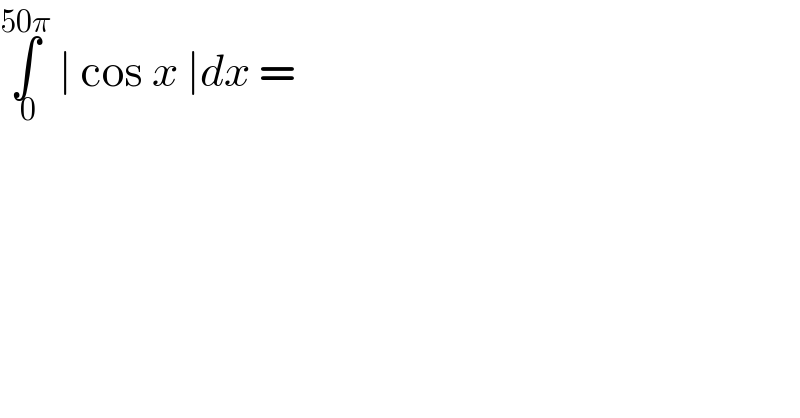
$$\underset{\:\mathrm{0}} {\overset{\mathrm{50}\pi} {\int}}\:\mid\:\mathrm{cos}\:{x}\:\mid{dx}\:= \\ $$
Commented by jagoll last updated on 25/Mar/20
![100×∫ _0 ^(π/2) cos x dx = 100 × [ sin x ]^(π/2) _( 0) = 100](https://www.tinkutara.com/question/Q85850.png)
$$\mathrm{100}×\int\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\:}}\mathrm{cos}\:\mathrm{x}\:\mathrm{dx}\: \\ $$$$=\:\mathrm{100}\:×\:\left[\:\mathrm{sin}\:\mathrm{x}\:\right]\underset{\:\:\mathrm{0}} {\:}^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\:\mathrm{100} \\ $$
Commented by mathmax by abdo last updated on 25/Mar/20
![I =Σ_(k=0) ^(49) ∫_(kπ) ^((k+1)π) ∣cosx∣dx =_(x=kπ +u) Σ_(k=0) ^(49) ∫_0 ^π ∣cos(kπ+u)∣ du =Σ_(k=0) ^(49) ∫_0 ^π ∣cosu∣ du =Σ_(k=0) ^(49) (∫_0 ^(π/2) cosu du −∫_(π/2) ^π cosu du) 50[sinu]_0 ^(π/2) −50[sinu]_(π/2) ^π =50 −50(−1) =50 +50 =100 ⇒I =100](https://www.tinkutara.com/question/Q85870.png)
$${I}\:=\sum_{{k}=\mathrm{0}} ^{\mathrm{49}} \:\:\:\int_{{k}\pi} ^{\left({k}+\mathrm{1}\right)\pi} \:\:\:\mid{cosx}\mid{dx}\:=_{{x}={k}\pi\:+{u}} \:\:\sum_{{k}=\mathrm{0}} ^{\mathrm{49}} \:\int_{\mathrm{0}} ^{\pi} \mid{cos}\left({k}\pi+{u}\right)\mid\:{du} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{49}} \:\int_{\mathrm{0}} ^{\pi} \mid{cosu}\mid\:{du}\:=\sum_{{k}=\mathrm{0}} ^{\mathrm{49}} \:\left(\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cosu}\:{du}\:−\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:{cosu}\:{du}\right) \\ $$$$\mathrm{50}\left[{sinu}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\mathrm{50}\left[{sinu}\right]_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:=\mathrm{50}\:−\mathrm{50}\left(−\mathrm{1}\right)\:=\mathrm{50}\:+\mathrm{50}\:=\mathrm{100} \\ $$$$\Rightarrow{I}\:=\mathrm{100} \\ $$
