Question Number 48105 by lhfgfgjokf last updated on 19/Nov/18
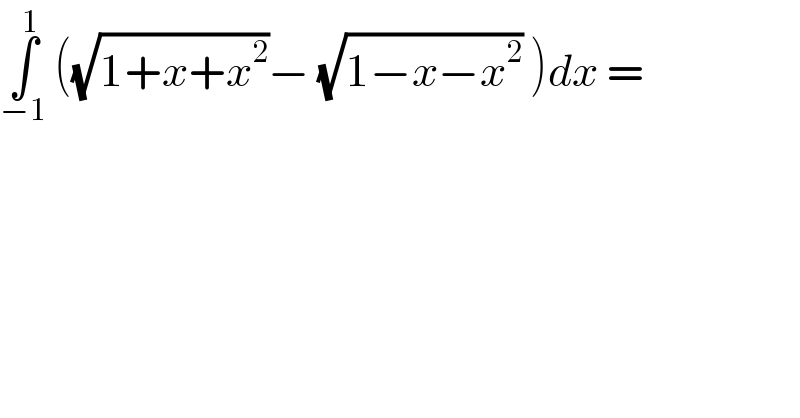
$$\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\:\left(\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }−\:\sqrt{\mathrm{1}−{x}−{x}^{\mathrm{2}} }\:\right){dx}\:= \\ $$
Commented by maxmathsup by imad last updated on 19/Nov/18
![I =H−K with H =∫_(−1) ^1 (√(x^2 +x+1))dx H = ∫_(−1) ^1 (√((x+(1/2))^2 +(3/4)))dx =_(x+(1/2)=((√3)/2)sh(t)) ∫_(−argsh((1/( (√3))))) ^(argsh((√3))) ((√3)/2) ch(t)((√3)/2)ch(t)dt =(3/4) ∫_(−ln((1/( (√3)))+(2/( (√3))))) ^(ln((√3)+2)) ((1+ch(2t))/2) dt =(3/8){ln((√3)+2)+ln((√3))} +(3/(16))[sh(2t)]_(−ln((√3))) ^(ln(2+(√3))) =(3/8){ln(2+(√3))+ln((√3))}+(3/(32)){e^(2t) −e^(−2t) ]_(−ln((√3))) ^(ln(2+(√3))) =(3/8){ln(2+(√3)) +ln((√3))}+(3/(32)){(2+(√3))^2 −(1/((2+(√3))^2 )) −( (1/(((√3))^2 )) +((√3))^2 )}](https://www.tinkutara.com/question/Q48134.png)
$${I}\:={H}−{K}\:{with}\:{H}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$${H}\:=\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}{dx}\:=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)} \:\:\:\:\int_{−{argsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)} ^{{argsh}\left(\sqrt{\mathrm{3}}\right)} \frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{ch}\left({t}\right)\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right){dt} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\:\int_{−{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\right)} ^{{ln}\left(\sqrt{\mathrm{3}}+\mathrm{2}\right)} \:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\:{dt}\:=\frac{\mathrm{3}}{\mathrm{8}}\left\{{ln}\left(\sqrt{\mathrm{3}}+\mathrm{2}\right)+{ln}\left(\sqrt{\mathrm{3}}\right)\right\} \\ $$$$+\frac{\mathrm{3}}{\mathrm{16}}\left[{sh}\left(\mathrm{2}{t}\right)\right]_{−{ln}\left(\sqrt{\mathrm{3}}\right)} ^{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} \:=\frac{\mathrm{3}}{\mathrm{8}}\left\{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)+{ln}\left(\sqrt{\mathrm{3}}\right)\right\}+\frac{\mathrm{3}}{\mathrm{32}}\left\{{e}^{\mathrm{2}{t}} −{e}^{−\mathrm{2}{t}} \right]_{−{ln}\left(\sqrt{\mathrm{3}}\right)} ^{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\left\{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\:+{ln}\left(\sqrt{\mathrm{3}}\right)\right\}+\frac{\mathrm{3}}{\mathrm{32}}\left\{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:−\left(\:\frac{\mathrm{1}}{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:+\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \right)\right\} \\ $$
Commented by maxmathsup by imad last updated on 19/Nov/18
![let calculate K =∫_(−1) ^1 (√(−x^2 −x +1)) K =∫_(−1) ^1 (√(1−(x^2 +x)))dx =∫_(−1) ^1 (√(1−((x+(1/2))^2 −(1/4))))dx =∫_(−1) ^1 (√((5/4)−(x+(1/2))^2 ))dx=_(x+(1/2)=((√5)/2)sint) ∫_(−arcsin((1/( (√5))))) ^(arcsin((3/( (√5))))) ((√5)/2) cost ((√5)/2) cost dt =(5/4) ∫_(−arcsin((1/( (√5))))) ^(arcsin((3/( (√5))))) cos^2 t dt =(5/8) ∫_(−arcsin((1/( (√5))))) ^(arcsin((3/( (√5) )))) (1+cos(2t))dt =(5/8){arcsin((3/( (√5))))+arcsin((1/( (√5))))}+(5/(16))[sin(2t)]_(−arcsin((1/( (√5)))))) ^(arcsin((3/( (√5) )))) =(5/8){arcsin((3/( (√5))))+arcsin((1/( (√5)))) +(5/(16)){sin(2arcsin((3/( (√5))))+sin(2arcsin((1/( (√5))))} so the value of I is known .](https://www.tinkutara.com/question/Q48135.png)
$${let}\:{calculate}\:{K}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{−{x}^{\mathrm{2}} −{x}\:+\mathrm{1}} \\ $$$${K}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}−\left({x}^{\mathrm{2}} +{x}\right)}{dx}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\mathrm{1}−\left(\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:−\frac{\mathrm{1}}{\mathrm{4}}\right)}{dx} \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{5}}{\mathrm{4}}−\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}{sint}} \:\:\:\int_{−{arcsin}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)} ^{{arcsin}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)} \:\:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:{cost}\:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:{cost}\:{dt} \\ $$$$=\frac{\mathrm{5}}{\mathrm{4}}\:\int_{−{arcsin}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)} ^{{arcsin}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)} {cos}^{\mathrm{2}} {t}\:{dt}\:=\frac{\mathrm{5}}{\mathrm{8}}\:\int_{−{arcsin}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)} ^{{arcsin}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}\:}\right)} \left(\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)\right){dt} \\ $$$$=\frac{\mathrm{5}}{\mathrm{8}}\left\{{arcsin}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)+{arcsin}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\right\}+\frac{\mathrm{5}}{\mathrm{16}}\left[{sin}\left(\mathrm{2}{t}\right)\right]_{−{arcsin}\left(\frac{\mathrm{1}}{\left.\:\sqrt{\mathrm{5}}\right)}\right)} ^{{arcsin}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}\:}\right)} \\ $$$$=\frac{\mathrm{5}}{\mathrm{8}}\left\{{arcsin}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)+{arcsin}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\:+\frac{\mathrm{5}}{\mathrm{16}}\left\{{sin}\left(\mathrm{2}{arcsin}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)+{sin}\left(\mathrm{2}{arcsin}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\right\}\right.\right.\right. \\ $$$${so}\:{the}\:{value}\:{of}\:{I}\:{is}\:{known}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18
![1+x+x^2 x^2 +2.x.(1/2)+(1/4)+(3/4) (x+(1/2))^2 +(((√3)/2))^2 1−x−x^2 1−(x^2 +2.x.(1/2)+(1/4)−(1/4)) 1+(1/4)−(x+(1/2))^2 =(((√5)/2))^2 −(x+(1/2))^2 formula ∫(√(a^2 +x^2 )) = ((x(√(x^2 +a^2 )) )/2)+(a^2 /2)ln(x+(√(x^2 +a^2 )) ) formula ∫(√(a^2 −x^2 )) dx= ((x(√(a^2 −x^2 )) )/2)+(a^2 /2)sin^(−1) ((x/a)) so first intregal is ∫_(−1) ^1 (√((x+(1/2))^2 +(((√3)/2))^2 )) ∣(((x+(1/2))(√((x+(1/2))^2 +(((√3)/2))^2 )))/2)+(((((√3)/2))^2 )/2)ln{(x+(1/2))+(√((x+(1/2))^2 +(((√3)/2))^2 )) ∣_(−1) ^1 [{(((1+(1/2))(√((9/4)+(3/4))) )/2)+(3/8)ln{((3/2))+(√3) }−{(((((−1)/2))(√((1/4)+(3/4))))/2)+(3/8)ln∣((−1)/2)+1∣}] =((((3/2))(√3))/2)+(3/8)ln{((3/2))+(√3) +(1/4)−(3/8)ln((1/2)) =((3(√3) +1)/4)+(3/8)ln3←value of first intregal calculation of second intregal ∫_(−1) ^1 (√((((√5)/2))^2 −(x+(1/2))^2 )) dx =∣(((x+(1/2))(√((((√5)/2))^2 −(x+(1/2))^2 )))/2)+(((((√5)/2))^2 )/2)sin^(−1) ((((x+(1/2)))/((√5)/2)))∣_(−1) ^1 =[{((((3/2))(√((5/4)−(9/4))) )/2)+(5/8)sin^(−1) ((3/( (√5))))}−{(((−(1/2))(√((5/4)−(1/4))))/2)+(5/8)sin^(−1) (((−1)/( (√5))))}] =[{((3i)/4)+(5/8)sin^(−1) ((3/( (√5))))}−{((−1)/4)+(5/8)sin^(−1) (((−1)/( (√5))))}] =((1+3i)/4)+(5/8){sin^(−1) ((3/( (√5))))+sin^(−1) ((1/( (√5))))} i=complex is coming so pls check the stdps required answer is [{((3(√3) +1)/4)+(3/8)ln3}−{((1+3i)/4)+(5/8){sin^(−1) ((3/( (√5))))+sin^(−1) ((1/( (√5))))}]](https://www.tinkutara.com/question/Q48112.png)
$$\mathrm{1}+{x}+{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}.{x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{1}−{x}−{x}^{\mathrm{2}} \\ $$$$\mathrm{1}−\left({x}^{\mathrm{2}} +\mathrm{2}.{x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}−\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${formula}\:\int\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:= \\ $$$$\frac{{x}\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\:}{\mathrm{2}}+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\:\right) \\ $$$${formula}\:\int\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{dx}= \\ $$$$\frac{{x}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:}{\mathrm{2}}+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right) \\ $$$${so}\:{first}\:{intregal}\:{is}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\: \\ $$$$\mid\frac{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \:}}{\mathrm{2}}+\frac{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}{ln}\left\{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\mid_{−\mathrm{1}} ^{\mathrm{1}} \right. \\ $$$$\left[\left\{\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}}\:}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{8}}{ln}\left\{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\sqrt{\mathrm{3}}\:\right\}−\left\{\frac{\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{8}}{ln}\mid\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}\mid\right\}\right]\right. \\ $$$$=\frac{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{8}}{ln}\left\{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\sqrt{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{8}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right. \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{3}}\:+\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{8}}{ln}\mathrm{3}\leftarrow{value}\:{of}\:{first}\:{intregal} \\ $$$${calculation}\:{of}\:{second}\:{intregal} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:{dx} \\ $$$$=\mid\frac{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }}{\mathrm{2}}+\frac{\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}}\right)\mid_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$=\left[\left\{\frac{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{5}}{\mathrm{4}}−\frac{\mathrm{9}}{\mathrm{4}}}\:}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{8}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)\right\}−\left\{\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{5}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{8}}{sin}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\right\}\right] \\ $$$$=\left[\left\{\frac{\mathrm{3}{i}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{8}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)\right\}−\left\{\frac{−\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{8}}{sin}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\right\}\right] \\ $$$$=\frac{\mathrm{1}+\mathrm{3}{i}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{8}}\left\{{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)+{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\right\} \\ $$$${i}={complex}\:{is}\:{coming}\:{so}\:{pls}\:{check}\:{the}\:{stdps} \\ $$$${required}\:{answer}\:{is}\: \\ $$$$\left[\left\{\frac{\mathrm{3}\sqrt{\mathrm{3}}\:+\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{8}}{ln}\mathrm{3}\right\}−\left\{\frac{\mathrm{1}+\mathrm{3}{i}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{8}}\left\{{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{5}}}\right)+{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\right\}\right]\right. \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 19/Nov/18
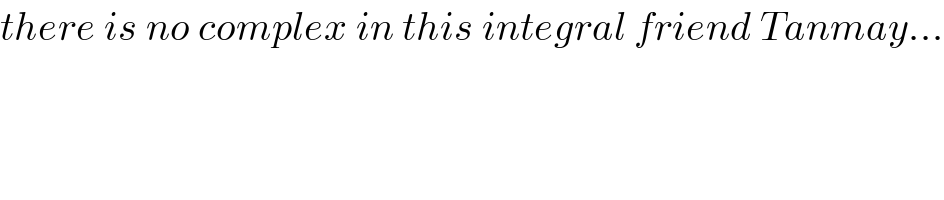
$${there}\:{is}\:{no}\:{complex}\:{in}\:{this}\:{integral}\:{friend}\:{Tanmay}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

$$\sqrt{\frac{\mathrm{5}}{\mathrm{4}}−\frac{\mathrm{9}}{\mathrm{4}}}\: \\ $$$$=\sqrt{−\mathrm{1}}\:\:{iscoming}\:\:{so}\:{pls}\:{check}.. \\ $$
Commented by MJS last updated on 19/Nov/18
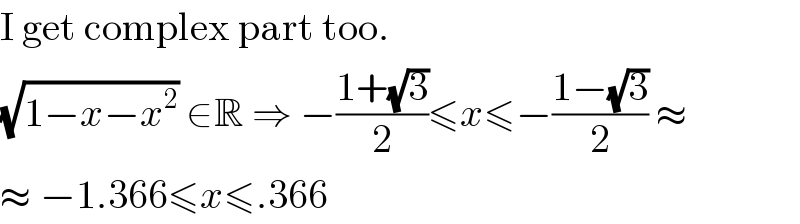
$$\mathrm{I}\:\mathrm{get}\:\mathrm{complex}\:\mathrm{part}\:\mathrm{too}. \\ $$$$\sqrt{\mathrm{1}−{x}−{x}^{\mathrm{2}} }\:\in\mathbb{R}\:\Rightarrow\:−\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}\leqslant{x}\leqslant−\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}}\:\approx \\ $$$$\approx\:−\mathrm{1}.\mathrm{366}\leqslant{x}\leqslant.\mathrm{366} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

$${thank}\:{you}\:{sir}…. \\ $$
