Question Number 83145 by 09658867628 last updated on 28/Feb/20
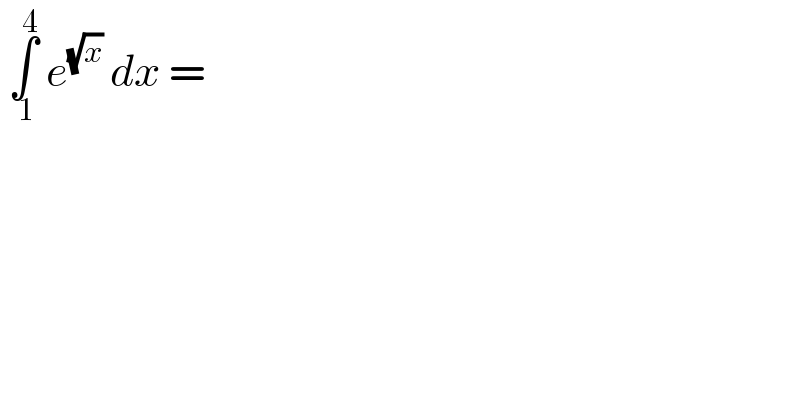
$$\:\underset{\:\mathrm{1}} {\overset{\mathrm{4}} {\int}}\:{e}^{\sqrt{{x}}} \:{dx}\:= \\ $$
Commented by mathmax by abdo last updated on 28/Feb/20
![I=∫_1 ^4 e^(√x) dx changement (√x)=t give I=∫_1 ^2 e^t (2t)dt =2 ∫_1 ^2 t e^t dt =_(byparts) 2{ [te^t ]_1 ^2 −∫_1 ^2 e^t dt} =2{2e^2 −e −(e^2 −e)} =2{e^2 } ⇒I =2e^2](https://www.tinkutara.com/question/Q83152.png)
$${I}=\int_{\mathrm{1}} ^{\mathrm{4}} \:{e}^{\sqrt{{x}}} {dx}\:\:{changement}\:\sqrt{{x}}={t}\:{give} \\ $$$${I}=\int_{\mathrm{1}} ^{\mathrm{2}} \:{e}^{{t}} \left(\mathrm{2}{t}\right){dt}\:=\mathrm{2}\:\int_{\mathrm{1}} ^{\mathrm{2}} \:{t}\:{e}^{{t}} \:{dt}\:=_{{byparts}} \:\:\mathrm{2}\left\{\:\left[{te}^{{t}} \right]_{\mathrm{1}} ^{\mathrm{2}} \:−\int_{\mathrm{1}} ^{\mathrm{2}} \:{e}^{{t}} \:{dt}\right\} \\ $$$$=\mathrm{2}\left\{\mathrm{2}{e}^{\mathrm{2}} −{e}\:−\left({e}^{\mathrm{2}} −{e}\right)\right\}\:=\mathrm{2}\left\{{e}^{\mathrm{2}} \right\}\:\Rightarrow{I}\:=\mathrm{2}{e}^{\mathrm{2}} \\ $$
Answered by Kunal12588 last updated on 28/Feb/20
![(√x)=t dx=2tdt I=2∫_1 ^2 te^t dt=2{[te^t ]_1 ^2 −∫_1 ^2 e^t dt} ⇒I=2{2e^2 −e−[e^t ]_1 ^2 } ⇒I=2{2e^2 −e−e^2 +e} ⇒I=2e^2 ∫_( 1) ^4 e^(√x) dx =2e^2 ; i hope this is correct](https://www.tinkutara.com/question/Q83150.png)
$$\sqrt{{x}}={t} \\ $$$${dx}=\mathrm{2}{tdt} \\ $$$${I}=\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{2}} {te}^{{t}} {dt}=\mathrm{2}\left\{\left[{te}^{{t}} \right]_{\mathrm{1}} ^{\mathrm{2}} −\int_{\mathrm{1}} ^{\mathrm{2}} {e}^{{t}} {dt}\right\} \\ $$$$\Rightarrow{I}=\mathrm{2}\left\{\mathrm{2}{e}^{\mathrm{2}} −{e}−\left[{e}^{{t}} \right]_{\mathrm{1}} ^{\mathrm{2}} \right\} \\ $$$$\Rightarrow{I}=\mathrm{2}\left\{\mathrm{2}{e}^{\mathrm{2}} −{e}−{e}^{\mathrm{2}} +{e}\right\} \\ $$$$\Rightarrow{I}=\mathrm{2}{e}^{\mathrm{2}} \\ $$$$\:\underset{\:\mathrm{1}} {\overset{\mathrm{4}} {\int}}\:{e}^{\sqrt{{x}}} \:{dx}\:=\mathrm{2}{e}^{\mathrm{2}} ;\:{i}\:{hope}\:{this}\:{is}\:{correct} \\ $$
