Question Number 54028 by qw last updated on 28/Jan/19
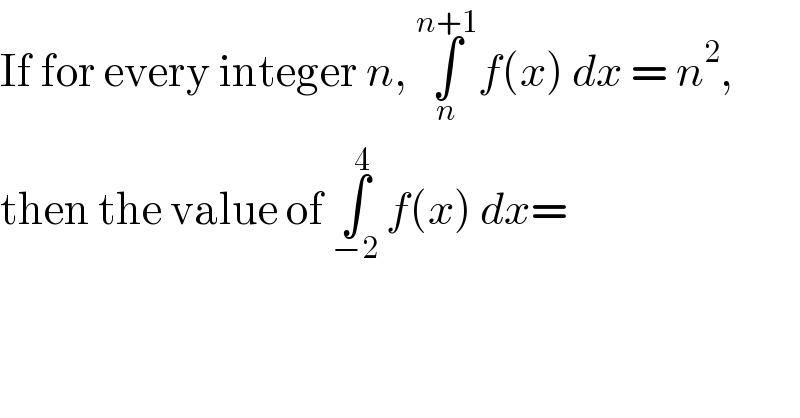
$$\mathrm{If}\:\mathrm{for}\:\mathrm{every}\:\mathrm{integer}\:{n},\:\underset{{n}} {\overset{{n}+\mathrm{1}} {\int}}{f}\left({x}\right)\:{dx}\:=\:{n}^{\mathrm{2}} , \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\underset{−\mathrm{2}} {\overset{\mathrm{4}} {\int}}\:{f}\left({x}\right)\:{dx}= \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Jan/19
![∫_(−2) ^4 f(x)dx ∫_(−2) ^(−2+1) f(x)dx+∫_(−1) ^(−1+1) f(x)dx+∫_0 ^(0+1) f(x)dx+∫_1 ^(1+1) f(x)dx+∫_2 ^(2+1) f(x)dx+∫_3 ^(3+1) f(x)dx [(−2)^2 +(−1)^2 +(0)^2 +(1)^2 +(2)^2 +(3)^2 ] =4+1+0+1+4+9 =19](https://www.tinkutara.com/question/Q54041.png)
$$\int_{−\mathrm{2}} ^{\mathrm{4}} {f}\left({x}\right){dx} \\ $$$$\int_{−\mathrm{2}} ^{−\mathrm{2}+\mathrm{1}} {f}\left({x}\right){dx}+\int_{−\mathrm{1}} ^{−\mathrm{1}+\mathrm{1}} {f}\left({x}\right){dx}+\int_{\mathrm{0}} ^{\mathrm{0}+\mathrm{1}} {f}\left({x}\right){dx}+\int_{\mathrm{1}} ^{\mathrm{1}+\mathrm{1}} {f}\left({x}\right){dx}+\int_{\mathrm{2}} ^{\mathrm{2}+\mathrm{1}} {f}\left({x}\right){dx}+\int_{\mathrm{3}} ^{\mathrm{3}+\mathrm{1}} {f}\left({x}\right){dx} \\ $$$$\left[\left(−\mathrm{2}\right)^{\mathrm{2}} +\left(−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{0}\right)^{\mathrm{2}} +\left(\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{3}\right)^{\mathrm{2}} \right] \\ $$$$=\mathrm{4}+\mathrm{1}+\mathrm{0}+\mathrm{1}+\mathrm{4}+\mathrm{9} \\ $$$$=\mathrm{19} \\ $$
