Question Number 7522 by Little last updated on 02/Sep/16
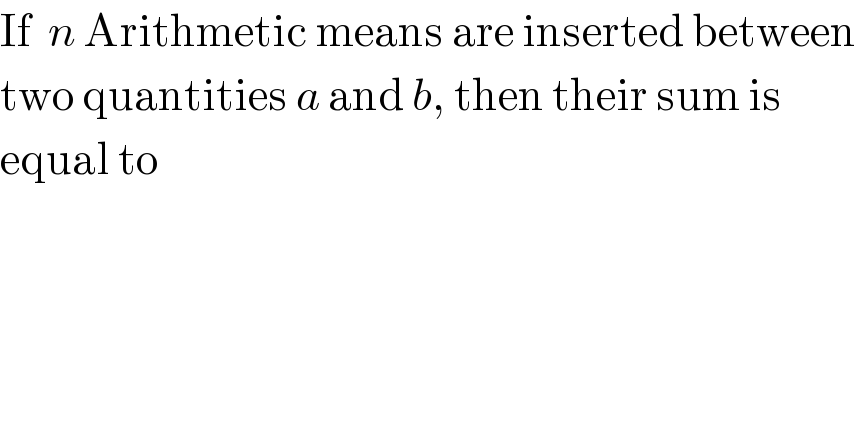
$$\mathrm{If}\:\:{n}\:\mathrm{Arithmetic}\:\mathrm{means}\:\mathrm{are}\:\mathrm{inserted}\:\mathrm{between} \\ $$$$\mathrm{two}\:\mathrm{quantities}\:{a}\:\mathrm{and}\:{b},\:\mathrm{then}\:\mathrm{their}\:\mathrm{sum}\:\mathrm{is} \\ $$$$\mathrm{equal}\:\mathrm{to} \\ $$
Commented by sandy_suhendra last updated on 02/Sep/16

$$\frac{{n}+\mathrm{2}}{\mathrm{2}}\:\left({a}+{b}\right) \\ $$
Commented by Rohit last updated on 03/Sep/16

$$\frac{{a}+{c}}{\mathrm{2}}={b} \\ $$
Answered by Rasheed Soomro last updated on 02/Sep/16
![Let A_1 ,A_2 ,A_3 ,...A_n are n AM ′s between a and b. a,A_1 ,A_2 ,A_3 ,...A_n ,b are in AP Let d be common fiffrrnce a+(n+2−1)d =(n+2)th term=b d=((b−a)/(n+1)) A_1 =a+((b−a)/(n+1)) , A_2 =a+2(((b−a)/(n+1))) , A_3 =a+3(((b−a)/(n+1))) ,.... A_n =a+n(((b−a)/(n+1))) S=(n/2)[2a+(n−1)d] S=(n/2)[2A_1 +(n−1)d] S=(n/2)[2(a+((b−a)/(n+1)))+(n−1)(((b−a)/(n+1)))] S=(n/2)[2a+2(((b−a)/(n+1)))+(n−1)(((b−a)/(n+1)))] S=(n/2)[2a+(((b−a)/(n+1)))[2+n−1]] S=(n/2)[2a+(((b−a)/(n+1)))[n+1]] S=(n/2)[2a+b−a] S=(n/2)[a+b]](https://www.tinkutara.com/question/Q7539.png)
$${Let}\:{A}_{\mathrm{1}} ,{A}_{\mathrm{2}} ,{A}_{\mathrm{3}} ,…{A}_{{n}} \:{are}\:{n}\:{AM}\:'{s}\:{between}\:{a}\:{and}\:{b}. \\ $$$${a},{A}_{\mathrm{1}} ,{A}_{\mathrm{2}} ,{A}_{\mathrm{3}} ,…{A}_{{n}} ,{b}\:{are}\:{in}\:{AP} \\ $$$${Let}\:{d}\:{be}\:{common}\:{fiffrrnce} \\ $$$${a}+\left({n}+\mathrm{2}−\mathrm{1}\right){d}\:=\left({n}+\mathrm{2}\right){th}\:{term}={b} \\ $$$$\:\:\:\:\:\:\:{d}=\frac{{b}−{a}}{{n}+\mathrm{1}} \\ $$$${A}_{\mathrm{1}} ={a}+\frac{{b}−{a}}{{n}+\mathrm{1}}\:\:,\:\:{A}_{\mathrm{2}} ={a}+\mathrm{2}\left(\frac{{b}−{a}}{{n}+\mathrm{1}}\right)\:\:,\:\:{A}_{\mathrm{3}} ={a}+\mathrm{3}\left(\frac{{b}−{a}}{{n}+\mathrm{1}}\right)\:\:,…. \\ $$$${A}_{{n}} ={a}+{n}\left(\frac{{b}−{a}}{{n}+\mathrm{1}}\right) \\ $$$${S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right] \\ $$$${S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{A}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){d}\right] \\ $$$${S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}\left({a}+\frac{{b}−{a}}{{n}+\mathrm{1}}\right)+\left({n}−\mathrm{1}\right)\left(\frac{{b}−{a}}{{n}+\mathrm{1}}\right)\right] \\ $$$${S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}+\mathrm{2}\left(\frac{{b}−{a}}{{n}+\mathrm{1}}\right)+\left({n}−\mathrm{1}\right)\left(\frac{{b}−{a}}{{n}+\mathrm{1}}\right)\right] \\ $$$${S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}+\left(\frac{{b}−{a}}{{n}+\mathrm{1}}\right)\left[\mathrm{2}+{n}−\mathrm{1}\right]\right] \\ $$$${S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}+\left(\frac{{b}−{a}}{{n}+\mathrm{1}}\right)\left[{n}+\mathrm{1}\right]\right] \\ $$$${S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}+{b}−{a}\right] \\ $$$${S}=\frac{{n}}{\mathrm{2}}\left[{a}+{b}\right] \\ $$$$ \\ $$
Commented by sandy_suhendra last updated on 03/Sep/16
![what′s the meaning of the question? A_1 +A_2 +...+An or a+A_1 +A_2 +...+A_n +b ? Sorry, my English is poor if a+A_1 +...A_n +b in a, A_1 , A_2 , ..., An, b there are (n+2) terms so S=(n/2)[2a+(n−1)d] becomes S=((n+2)/2)[2a+(n+2−1)d]](https://www.tinkutara.com/question/Q7572.png)
$${what}'{s}\:{the}\:{meaning}\:{of}\:{the}\:{question}? \\ $$$${A}_{\mathrm{1}} +{A}_{\mathrm{2}} +…+{An}\:\:{or}\:\:{a}+{A}_{\mathrm{1}} +{A}_{\mathrm{2}} +…+{A}_{{n}} +{b}\:\:? \\ $$$${Sorry},\:{my}\:{English}\:{is}\:{poor} \\ $$$${if}\:{a}+{A}_{\mathrm{1}} +…{A}_{{n}} +{b} \\ $$$${in}\:{a},\:{A}_{\mathrm{1}} ,\:{A}_{\mathrm{2}} ,\:…,\:{An},\:{b}\:\:{there}\:{are}\:\left({n}+\mathrm{2}\right)\:{terms} \\ $$$${so}\:\:{S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right]\:{becomes}\:{S}=\frac{{n}+\mathrm{2}}{\mathrm{2}}\left[\mathrm{2}{a}+\left({n}+\mathrm{2}−\mathrm{1}\right){d}\right] \\ $$
Commented by Rasheed Soomro last updated on 04/Sep/16

$${May}\:{be}\:{you}\:{are}\:{right}.\:{But} \\ $$$${by}\:“{their}\:{sum}''\:{I}\:{understood} \\ $$$$'{the}\:{sum}\:{of}\:{AM}\:'{s}'\:{here}. \\ $$$$ \\ $$
