Question Number 49459 by Pk1167156@gmail.com last updated on 07/Dec/18
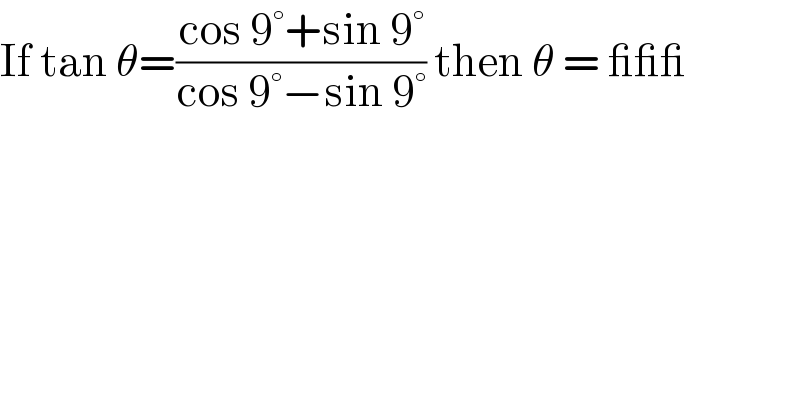
$$\mathrm{If}\:\mathrm{tan}\:\theta=\frac{\mathrm{cos}\:\mathrm{9}°+\mathrm{sin}\:\mathrm{9}°}{\mathrm{cos}\:\mathrm{9}°−\mathrm{sin}\:\mathrm{9}°}\:\mathrm{then}\:\theta\:=\:\_\_\_ \\ $$
Answered by math1967 last updated on 07/Dec/18
![tanθ=((cos9+cos(90−9))/(cos9−cos(90−9))) tanθ=((cos9+cos81)/(cos9−cos81)) tanθ=((2cos45.cos36)/(2sin45.sin36)) tanθ=cot36 [∵cos45=sin45] tanθ=cot36 tanθ=tan(90−36) tanθ=tan54 ∴θ=54 ans](https://www.tinkutara.com/question/Q49471.png)
$${tan}\theta=\frac{{cos}\mathrm{9}+{cos}\left(\mathrm{90}−\mathrm{9}\right)}{{cos}\mathrm{9}−{cos}\left(\mathrm{90}−\mathrm{9}\right)} \\ $$$${tan}\theta=\frac{{cos}\mathrm{9}+{cos}\mathrm{81}}{{cos}\mathrm{9}−{cos}\mathrm{81}} \\ $$$${tan}\theta=\frac{\mathrm{2}{cos}\mathrm{45}.{cos}\mathrm{36}}{\mathrm{2}{sin}\mathrm{45}.{sin}\mathrm{36}} \\ $$$${tan}\theta={cot}\mathrm{36}\:\:\:\:\left[\because{cos}\mathrm{45}={sin}\mathrm{45}\right] \\ $$$${tan}\theta={cot}\mathrm{36} \\ $$$${tan}\theta={tan}\left(\mathrm{90}−\mathrm{36}\right) \\ $$$${tan}\theta={tan}\mathrm{54}\:\therefore\theta=\mathrm{54}\:{ans} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Dec/18
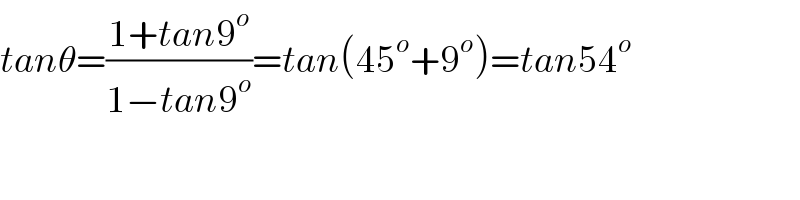
$${tan}\theta=\frac{\mathrm{1}+{tan}\mathrm{9}^{{o}} }{\mathrm{1}−{tan}\mathrm{9}^{{o}} }={tan}\left(\mathrm{45}^{{o}} +\mathrm{9}^{{o}} \right)={tan}\mathrm{54}^{{o}} \\ $$
