Question Number 62612 by hovea cw last updated on 23/Jun/19
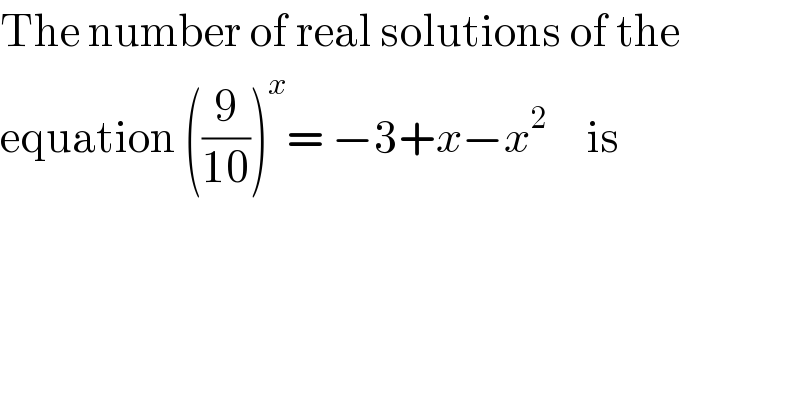
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\left(\frac{\mathrm{9}}{\mathrm{10}}\right)^{{x}} =\:−\mathrm{3}+{x}−{x}^{\mathrm{2}} \:\:\:\:\:\mathrm{is} \\ $$
Answered by tanmay last updated on 23/Jun/19
![−3+x−x^2 =−x^2 +x−3 =−(x^2 −x+3) =−(x^2 −2×x×(1/2)+(1/4)−(1/4)+3) =−(x−(1/2))^2 +(1/4)−3 =−(x−(1/2))^2 −((11)/4)<0 [always −ve] but ((9/(10)))^x >0 [aleays +ve] so no real solution](https://www.tinkutara.com/question/Q62619.png)
$$−\mathrm{3}+{x}−{x}^{\mathrm{2}} \\ $$$$=−{x}^{\mathrm{2}} +{x}−\mathrm{3} \\ $$$$=−\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right) \\ $$$$=−\left({x}^{\mathrm{2}} −\mathrm{2}×{x}×\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{3}\right) \\ $$$$=−\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{3} \\ $$$$=−\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{11}}{\mathrm{4}}<\mathrm{0}\:\left[{always}\:−{ve}\right] \\ $$$${but}\:\left(\frac{\mathrm{9}}{\mathrm{10}}\right)^{{x}} >\mathrm{0}\:\left[{aleays}\:+{ve}\right] \\ $$$${so}\:{no}\:{real}\:{solution} \\ $$
