Question Number 55787 by gunawan last updated on 04/Mar/19
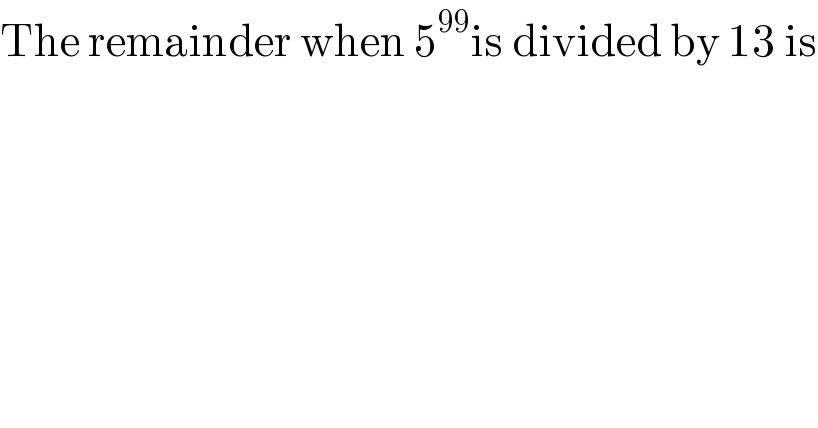
$$\mathrm{The}\:\mathrm{remainder}\:\mathrm{when}\:\mathrm{5}^{\mathrm{99}} \mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{13}\:\mathrm{is} \\ $$
Answered by MJS last updated on 04/Mar/19
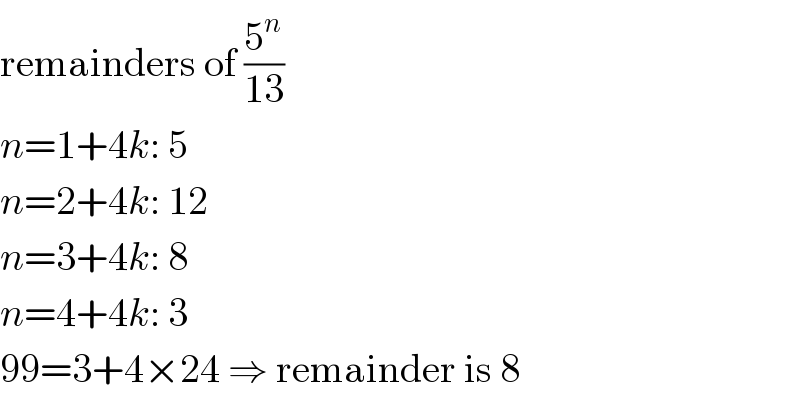
$$\mathrm{remainders}\:\mathrm{of}\:\frac{\mathrm{5}^{{n}} }{\mathrm{13}} \\ $$$${n}=\mathrm{1}+\mathrm{4}{k}:\:\mathrm{5} \\ $$$${n}=\mathrm{2}+\mathrm{4}{k}:\:\mathrm{12} \\ $$$${n}=\mathrm{3}+\mathrm{4}{k}:\:\mathrm{8} \\ $$$${n}=\mathrm{4}+\mathrm{4}{k}:\:\mathrm{3} \\ $$$$\mathrm{99}=\mathrm{3}+\mathrm{4}×\mathrm{24}\:\Rightarrow\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{8} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Mar/19
![trying other way 5^(99) =(5^3 )^(33) =(125)^(33) =(9×13+8)^(33) =(9×13)^(33) +33c_1 (9×13)^(32) ×8+...+8^(33) =f(13)+(512)^(11) =f(13)+(13×39+5)^(11) =f(13)+g(13)+5^(11) =f(13+g(13)+5×(5^2 )^5 =f(13)+g(13)+5×(13+12)^5 =f(13)+g(13)+5×[13^5 +5c_1 13^4 +...+12^5 ] =f(13)+g(13)+5×h(13)+5×12^5 =f(13)+g(13)+5×h(13)+5×(144)^3 =f(13)+g(13)+5×h(13)+5×(13×11+1)^3 =f(13)+g(13)+5×h(13)+5×[(13×11)^3 +3×(13×11)^2 +3×(13×11)×1^2 +1^3 ] =f(13)+g(13)+5×h(13)+5×γ(13)+5×1^3 so in my calculation remaider is 5](https://www.tinkutara.com/question/Q55810.png)
$${trying}\:{other}\:{way} \\ $$$$\mathrm{5}^{\mathrm{99}} \\ $$$$=\left(\mathrm{5}^{\mathrm{3}} \right)^{\mathrm{33}} \\ $$$$=\left(\mathrm{125}\right)^{\mathrm{33}} \\ $$$$=\left(\mathrm{9}×\mathrm{13}+\mathrm{8}\right)^{\mathrm{33}} \\ $$$$=\left(\mathrm{9}×\mathrm{13}\right)^{\mathrm{33}} +\mathrm{33}{c}_{\mathrm{1}} \left(\mathrm{9}×\mathrm{13}\right)^{\mathrm{32}} ×\mathrm{8}+…+\mathrm{8}^{\mathrm{33}} \\ $$$$={f}\left(\mathrm{13}\right)+\left(\mathrm{512}\right)^{\mathrm{11}} \\ $$$$={f}\left(\mathrm{13}\right)+\left(\mathrm{13}×\mathrm{39}+\mathrm{5}\right)^{\mathrm{11}} \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}^{\mathrm{11}} \\ $$$$={f}\left(\mathrm{13}+{g}\left(\mathrm{13}\right)+\mathrm{5}×\left(\mathrm{5}^{\mathrm{2}} \right)^{\mathrm{5}} \right. \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×\left(\mathrm{13}+\mathrm{12}\right)^{\mathrm{5}} \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×\left[\mathrm{13}^{\mathrm{5}} +\mathrm{5}{c}_{\mathrm{1}} \mathrm{13}^{\mathrm{4}} +…+\mathrm{12}^{\mathrm{5}} \right] \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×{h}\left(\mathrm{13}\right)+\mathrm{5}×\mathrm{12}^{\mathrm{5}} \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×{h}\left(\mathrm{13}\right)+\mathrm{5}×\left(\mathrm{144}\right)^{\mathrm{3}} \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×{h}\left(\mathrm{13}\right)+\mathrm{5}×\left(\mathrm{13}×\mathrm{11}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×{h}\left(\mathrm{13}\right)+\mathrm{5}×\left[\left(\mathrm{13}×\mathrm{11}\right)^{\mathrm{3}} +\mathrm{3}×\left(\mathrm{13}×\mathrm{11}\right)^{\mathrm{2}} +\mathrm{3}×\left(\mathrm{13}×\mathrm{11}\right)×\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{3}} \right] \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×{h}\left(\mathrm{13}\right)+\mathrm{5}×\gamma\left(\mathrm{13}\right)+\mathrm{5}×\mathrm{1}^{\mathrm{3}} \\ $$$${so}\:{in}\:{my}\:{calculation}\:{remaider}\:{is}\:\mathrm{5} \\ $$
Commented by mr W last updated on 05/Mar/19

$${here}\:{is}\:{wrong}\:{sir}! \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×{h}\left(\mathrm{13}\right)+\mathrm{5}×\mathrm{12}^{\mathrm{5}} \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×{h}\left(\mathrm{13}\right)+\mathrm{5}×\left(\mathrm{144}\right)^{\mathrm{3}} \\ $$$${it}\:{should}\:{be}: \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×{h}\left(\mathrm{13}\right)+\mathrm{5}×\mathrm{12}×\left(\mathrm{144}\right)^{\mathrm{2}} \\ $$$$={f}\left(\mathrm{13}\right)+{g}\left(\mathrm{13}\right)+\mathrm{5}×{h}\left(\mathrm{13}\right)+\mathrm{60}×\left(\mathrm{13}×\mathrm{11}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=……+\mathrm{60} \\ $$$$=……+\mathrm{13}×\mathrm{4}+\mathrm{8} \\ $$$$=……+\mathrm{8} \\ $$$$\Rightarrow{remainder}\:{is}\:\mathrm{8}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 05/Mar/19
$${thank}\:{you}\:{sir}..{many}\:{many}\:{thanks}… \\ $$
