Menu Close

The-sum-of-the-last-eight-coefficients-in-the-expansion-of-1-x-16-is-2-15-

Tinku Tara 0 Comments
Pin




Question Number 55788 by gunawan last updated on 04/Mar/19
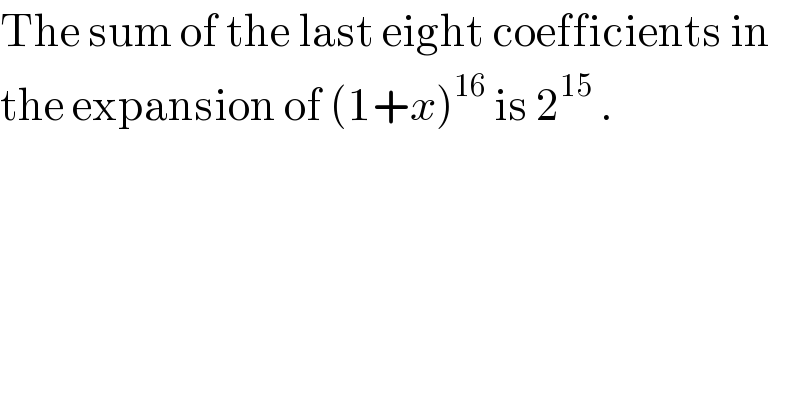
The sum of the last eight coefficients in the expansion of (1+x)^(16) is 2^(15) .
$$\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{last}\:\mathrm{eight}\:\mathrm{coefficients}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+{x}\right)^{\mathrm{16}} \:\mathrm{is}\:\mathrm{2}^{\mathrm{15}} \:. \\ $$
Commented by gunawan last updated on 04/Mar/19
True or false
$$\mathrm{True}\:\mathrm{or}\:\mathrm{false} \\ $$
Commented by maxmathsup by imad last updated on 04/Mar/19
we have (x+1)^(16) =Σ_(k=0) ^(16) C_(16) ^k x^k =Σ_(k=0) ^(16) a_k x^k ⇒ a_0 +a_1 +....+a_7 =Σ_(k=0) ^7 C_(16) ^k but if p(x)=a_0 +a_1 x +a_2 x^2 +...+a_n x^n ⇒ a_o +a_1 +....+a_n =p(1) and a_o +a_1 +...+a_p =p(1)−a_(p+1) −a_(p+2) −...−a_n in this case p(x)=(x+1)^(16) ⇒a_0 +a_1 +...+a_7 =p(1)−a_8 −a_9 −....−a_(16) but a_8 =C_(16) ^8 a_9 =C_(16) ^9 =C_(16) ^7 =a_7 , a_(10) =C_(16) ^(10) =C_(16) ^6 =a_6 , a_(16) =a_0 2(a_0 +a_1 +....+a_7 ) =p(1)−a_8 =2^(16) −C_(16) ^8 =2^(16) −((16!)/(8!8!)) =2^(16) −((16!)/((8!)^2 ))
$${we}\:{have}\:\left({x}+\mathrm{1}\right)^{\mathrm{16}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{16}} \:{C}_{\mathrm{16}} ^{{k}} \:{x}^{{k}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{16}} \:{a}_{{k}} {x}^{{k}} \:\Rightarrow \\ $$$${a}_{\mathrm{0}} +{a}_{\mathrm{1}} +….+{a}_{\mathrm{7}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{7}} \:{C}_{\mathrm{16}} ^{{k}} \:\:\:{but}\:{if}\:\:{p}\left({x}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}\:+{a}_{\mathrm{2}} {x}^{\mathrm{2}} \:+…+{a}_{{n}} {x}^{{n}} \:\Rightarrow \\ $$$${a}_{{o}} \:+{a}_{\mathrm{1}} +….+{a}_{{n}} ={p}\left(\mathrm{1}\right)\:{and}\:{a}_{{o}} \:+{a}_{\mathrm{1}} +…+{a}_{{p}} ={p}\left(\mathrm{1}\right)−{a}_{{p}+\mathrm{1}} −{a}_{{p}+\mathrm{2}} −…−{a}_{{n}} \:{in}\:{this}\:{case} \\ $$$${p}\left({x}\right)=\left({x}+\mathrm{1}\right)^{\mathrm{16}} \:\Rightarrow{a}_{\mathrm{0}} \:+{a}_{\mathrm{1}} +…+{a}_{\mathrm{7}} ={p}\left(\mathrm{1}\right)−{a}_{\mathrm{8}} −{a}_{\mathrm{9}} −….−{a}_{\mathrm{16}} \\ $$$${but}\:{a}_{\mathrm{8}} ={C}_{\mathrm{16}} ^{\mathrm{8}} \:\:\:\:\:{a}_{\mathrm{9}} ={C}_{\mathrm{16}} ^{\mathrm{9}} ={C}_{\mathrm{16}} ^{\mathrm{7}} ={a}_{\mathrm{7}} \:\:,\:\:{a}_{\mathrm{10}} ={C}_{\mathrm{16}} ^{\mathrm{10}} \:={C}_{\mathrm{16}} ^{\mathrm{6}} \:={a}_{\mathrm{6}} \:,\:\:{a}_{\mathrm{16}} ={a}_{\mathrm{0}} \\ $$$$\mathrm{2}\left({a}_{\mathrm{0}} \:+{a}_{\mathrm{1}} +….+{a}_{\mathrm{7}} \right)\:={p}\left(\mathrm{1}\right)−{a}_{\mathrm{8}} =\mathrm{2}^{\mathrm{16}} \:−{C}_{\mathrm{16}} ^{\mathrm{8}} \:=\mathrm{2}^{\mathrm{16}} −\frac{\mathrm{16}!}{\mathrm{8}!\mathrm{8}!} \\ $$$$=\mathrm{2}^{\mathrm{16}} −\frac{\mathrm{16}!}{\left(\mathrm{8}!\right)^{\mathrm{2}} } \\ $$
Commented by maxmathsup by imad last updated on 04/Mar/19
⇒a_0 +a_1 +....+a_7 =2^(15) −(1/2) ((16!)/((8!)^2 ))
$$\Rightarrow{a}_{\mathrm{0}} +{a}_{\mathrm{1}} +….+{a}_{\mathrm{7}} =\mathrm{2}^{\mathrm{15}} −\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{16}!}{\left(\mathrm{8}!\right)^{\mathrm{2}} } \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Mar/19
total terms=16+1=17 sum of coeffucients (1+x)^(16) =1+16c_1 x+16c_2 x^2 +16c_3 x^3 +..+16c_(16) x^(16) 2^(16) =16c_0 +16c_1 +...+16c_8 +16c_9 +16c_(10) +..+16c_(16) we have ti find the value of 16c_(16) +16c_(15) +16c_(14) +16c_(13) +16c_(12) +16c_(11) +16c_(10) +16c_9 =k again 16c_0 +16c_1 +16c_2 +16c_3 +16c_4 +16c_5 +16c_6 +16c_7 =k [since nc_r =nc_(n−r) ] now ninth term is 16c_8 x^8 →coeeficient=16c_8 so 2k+16c_8 =2^(16) 2k=2^(16) −((16!)/(8!8!)) k=2^(15) −(1/2)(((16!)/(8!8!))) required ans is2^(15) −(1/2)(((16!)/(8!8!))) pls check...
$${total}\:{terms}=\mathrm{16}+\mathrm{1}=\mathrm{17} \\ $$$${sum}\:{of}\:{coeffucients} \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{16}} =\mathrm{1}+\mathrm{16}{c}_{\mathrm{1}} {x}+\mathrm{16}{c}_{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{16}{c}_{\mathrm{3}} {x}^{\mathrm{3}} +..+\mathrm{16}{c}_{\mathrm{16}} {x}^{\mathrm{16}} \\ $$$$\mathrm{2}^{\mathrm{16}} =\mathrm{16}{c}_{\mathrm{0}} +\mathrm{16}{c}_{\mathrm{1}} +…+\mathrm{16}{c}_{\mathrm{8}} +\mathrm{16}{c}_{\mathrm{9}} +\mathrm{16}{c}_{\mathrm{10}} +..+\mathrm{16}{c}_{\mathrm{16}} \\ $$$${we}\:{have}\:{ti}\:{find}\:{the}\:{value}\:{of}\: \\ $$$$\mathrm{16}{c}_{\mathrm{16}} +\mathrm{16}{c}_{\mathrm{15}} +\mathrm{16}{c}_{\mathrm{14}} +\mathrm{16}{c}_{\mathrm{13}} +\mathrm{16}{c}_{\mathrm{12}} +\mathrm{16}{c}_{\mathrm{11}} +\mathrm{16}{c}_{\mathrm{10}} +\mathrm{16}{c}_{\mathrm{9}} ={k} \\ $$$${again} \\ $$$$\mathrm{16}{c}_{\mathrm{0}} +\mathrm{16}{c}_{\mathrm{1}} +\mathrm{16}{c}_{\mathrm{2}} +\mathrm{16}{c}_{\mathrm{3}} +\mathrm{16}{c}_{\mathrm{4}} +\mathrm{16}{c}_{\mathrm{5}} +\mathrm{16}{c}_{\mathrm{6}} +\mathrm{16}{c}_{\mathrm{7}} ={k} \\ $$$$\left[{since}\:{nc}_{{r}} ={nc}_{{n}−{r}} \right] \\ $$$${now} \\ $$$${ninth}\:{term}\:{is}\:\mathrm{16}{c}_{\mathrm{8}} {x}^{\mathrm{8}} \rightarrow{coeeficient}=\mathrm{16}{c}_{\mathrm{8}} \\ $$$${so}\:\mathrm{2}{k}+\mathrm{16}{c}_{\mathrm{8}} =\mathrm{2}^{\mathrm{16}} \\ $$$$\mathrm{2}{k}=\mathrm{2}^{\mathrm{16}} −\frac{\mathrm{16}!}{\mathrm{8}!\mathrm{8}!} \\ $$$${k}=\mathrm{2}^{\mathrm{15}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{16}!}{\mathrm{8}!\mathrm{8}!}\right) \\ $$$${required}\:{ans}\:{is}\mathrm{2}^{\mathrm{15}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{16}!}{\mathrm{8}!\mathrm{8}!}\right) \\ $$$${pls}\:{check}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *