Question Number 21549 by x² – y²@gmail.com last updated on 27/Sep/17

$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{expression}\: \\ $$$$\mathrm{3}\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)^{\mathrm{4}} +\mathrm{6}\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{4}\left(\mathrm{sin}^{\mathrm{6}} \theta+\mathrm{cos}^{\mathrm{6}} \theta\right)\:\:\mathrm{is} \\ $$
Answered by Tikufly last updated on 27/Sep/17
![Sol 3[(sinθ−cosθ)^2 ]^2 +6(1+2sinθcosθ) +4[(sin^2 θ)^3 +(cos^2 θ)^3 ] ⇒3(1−2sinθcosθ)^2 +6(1+sin2θ) +4[(sin^2 θ+cos^2 θ)^3 −3sin^2 θcos^2 θ(sin^2 θ+cos^2 θ)] ⇒3(1−sin2θ)^2 +6(1+sin2θ)+4(1−3sin^2 θcos^2 θ) ⇒3[(1+sin2θ)^2 −4sin2θ]+6(1+sin2θ)+4(1−(3/4)sin^2 2θ) ⇒3(1+sin2θ)^2 −12sin2θ+6+6sin2θ+4−3sin^2 2θ ⇒3(1+sin2θ)^2 +3−3sin^2 2θ+7−6sin2θ ⇒3(1+sin2θ)(1+sin2θ+1−sin2θ)+7−6sin2θ ⇒6(1+sin2θ)+7−6sin2θ ⇒6+6sin2θ+7−6sin2θ ⇒13](https://www.tinkutara.com/question/Q21561.png)
$$\mathrm{Sol} \\ $$$$\mathrm{3}\left[\left(\mathrm{sin}\theta−\mathrm{cos}\theta\right)^{\mathrm{2}} \right]^{\mathrm{2}} +\mathrm{6}\left(\mathrm{1}+\mathrm{2sin}\theta\mathrm{cos}\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{4}\left[\left(\mathrm{sin}^{\mathrm{2}} \theta\right)^{\mathrm{3}} +\left(\mathrm{cos}^{\mathrm{2}} \theta\right)^{\mathrm{3}} \right] \\ $$$$\Rightarrow\mathrm{3}\left(\mathrm{1}−\mathrm{2sin}\theta\mathrm{cos}\theta\right)^{\mathrm{2}} +\mathrm{6}\left(\mathrm{1}+\mathrm{sin2}\theta\right) \\ $$$$\:\:\:\:+\mathrm{4}\left[\left(\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta\right)^{\mathrm{3}} −\mathrm{3sin}^{\mathrm{2}} \theta\mathrm{cos}^{\mathrm{2}} \theta\left(\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta\right)\right] \\ $$$$\Rightarrow\mathrm{3}\left(\mathrm{1}−\mathrm{sin2}\theta\right)^{\mathrm{2}} +\mathrm{6}\left(\mathrm{1}+\mathrm{sin2}\theta\right)+\mathrm{4}\left(\mathrm{1}−\mathrm{3sin}^{\mathrm{2}} \theta\mathrm{cos}^{\mathrm{2}} \theta\right) \\ $$$$\Rightarrow\mathrm{3}\left[\left(\mathrm{1}+\mathrm{sin2}\theta\right)^{\mathrm{2}} −\mathrm{4sin2}\theta\right]+\mathrm{6}\left(\mathrm{1}+\mathrm{sin2}\theta\right)+\mathrm{4}\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \mathrm{2}\theta\right) \\ $$$$\Rightarrow\mathrm{3}\left(\mathrm{1}+\mathrm{sin2}\theta\right)^{\mathrm{2}} −\mathrm{12sin2}\theta+\mathrm{6}+\mathrm{6sin2}\theta+\mathrm{4}−\mathrm{3sin}^{\mathrm{2}} \mathrm{2}\theta \\ $$$$\Rightarrow\mathrm{3}\left(\mathrm{1}+\mathrm{sin2}\theta\right)^{\mathrm{2}} +\mathrm{3}−\mathrm{3sin}^{\mathrm{2}} \mathrm{2}\theta+\mathrm{7}−\mathrm{6sin2}\theta \\ $$$$\Rightarrow\mathrm{3}\left(\mathrm{1}+\mathrm{sin2}\theta\right)\left(\mathrm{1}+\mathrm{sin2}\theta+\mathrm{1}−\mathrm{sin2}\theta\right)+\mathrm{7}−\mathrm{6sin2}\theta \\ $$$$\Rightarrow\mathrm{6}\left(\mathrm{1}+\mathrm{sin2}\theta\right)+\mathrm{7}−\mathrm{6sin2}\theta \\ $$$$\Rightarrow\mathrm{6}+\mathrm{6sin2}\theta+\mathrm{7}−\mathrm{6sin2}\theta \\ $$$$\Rightarrow\mathrm{13} \\ $$
Commented by x² – y²@gmail.com last updated on 27/Sep/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$$$ \\ $$
Answered by $@ty@m last updated on 20/Oct/17
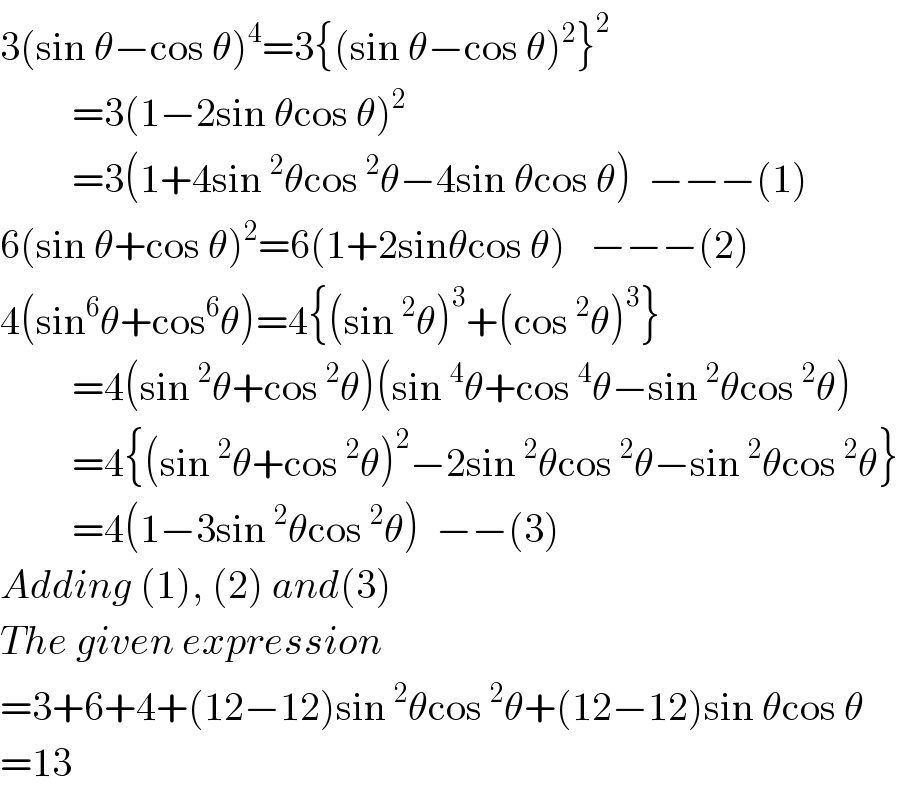
$$\mathrm{3}\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)^{\mathrm{4}} =\mathrm{3}\left\{\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{3}\left(\mathrm{1}−\mathrm{2sin}\:\theta\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{3}\left(\mathrm{1}+\mathrm{4sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta−\mathrm{4sin}\:\theta\mathrm{cos}\:\theta\right)\:\:−−−\left(\mathrm{1}\right) \\ $$$$\mathrm{6}\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\mathrm{6}\left(\mathrm{1}+\mathrm{2sin}\theta\mathrm{cos}\:\theta\right)\:\:\:−−−\left(\mathrm{2}\right) \\ $$$$\mathrm{4}\left(\mathrm{sin}^{\mathrm{6}} \theta+\mathrm{cos}^{\mathrm{6}} \theta\right)=\mathrm{4}\left\{\left(\mathrm{sin}\:^{\mathrm{2}} \theta\right)^{\mathrm{3}} +\left(\mathrm{cos}\:^{\mathrm{2}} \theta\right)^{\mathrm{3}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{4}\left(\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{cos}\:^{\mathrm{2}} \theta\right)\left(\mathrm{sin}\:^{\mathrm{4}} \theta+\mathrm{cos}\:^{\mathrm{4}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{4}\left\{\left(\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{cos}\:^{\mathrm{2}} \theta\right)^{\mathrm{2}} −\mathrm{2sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta\right\} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{4}\left(\mathrm{1}−\mathrm{3sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta\right)\:\:−−\left(\mathrm{3}\right) \\ $$$${Adding}\:\left(\mathrm{1}\right),\:\left(\mathrm{2}\right)\:{and}\left(\mathrm{3}\right) \\ $$$${The}\:{given}\:{expression} \\ $$$$=\mathrm{3}+\mathrm{6}+\mathrm{4}+\left(\mathrm{12}−\mathrm{12}\right)\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta+\left(\mathrm{12}−\mathrm{12}\right)\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$=\mathrm{13} \\ $$
Commented by $@ty@m last updated on 27/Sep/17

$${Thanks} \\ $$$${Corrected}…. \\ $$
Commented by x² – y²@gmail.com last updated on 27/Sep/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
