Question Number 53515 by 0955083339 last updated on 22/Jan/19
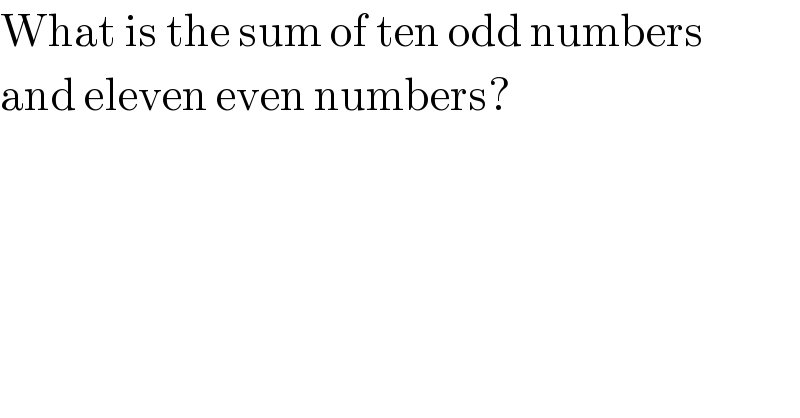
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{ten}\:\mathrm{odd}\:\mathrm{numbers} \\ $$$$\mathrm{and}\:\mathrm{eleven}\:\mathrm{even}\:\mathrm{numbers}? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Jan/19
![S_(odd) =1+3+5+...+[1+(10−1)2] S_(odd) =1+3+5+...+19 S_(odd) =19+17+15+...+1 add 2S_(odd) =20+20+20...ten times 2S_(odd) =20×10 S_(odd) =100 or direct formula S=(n/2)[2a+(n−1)d] =((10)/2)[2×1+(10−1)2] =100 S_(even) =2+4+6+...+[2+(11−1)2] S_(even) =2+4+6+...+22 S_(even) =22+20+18+...+2 add 2S_(even) =24+24+24...eleven times 2S_(even) =24×11 S_(even) =((24×11)/2)=132 or direct formula S_(even) =((11)/2)[2×2+(11−1)2] S_(even) =((11)/2)[24]=132](https://www.tinkutara.com/question/Q53539.png)
$${S}_{{odd}} =\mathrm{1}+\mathrm{3}+\mathrm{5}+…+\left[\mathrm{1}+\left(\mathrm{10}−\mathrm{1}\right)\mathrm{2}\right] \\ $$$${S}_{{odd}} =\mathrm{1}+\mathrm{3}+\mathrm{5}+…+\mathrm{19} \\ $$$${S}_{{odd}} =\mathrm{19}+\mathrm{17}+\mathrm{15}+…+\mathrm{1} \\ $$$${add} \\ $$$$\mathrm{2}{S}_{{odd}} =\mathrm{20}+\mathrm{20}+\mathrm{20}…{ten}\:{times} \\ $$$$\mathrm{2}{S}_{{odd}} =\mathrm{20}×\mathrm{10} \\ $$$${S}_{{odd}} =\mathrm{100} \\ $$$${or}\:{direct}\:{formula}\: \\ $$$${S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right] \\ $$$$=\frac{\mathrm{10}}{\mathrm{2}}\left[\mathrm{2}×\mathrm{1}+\left(\mathrm{10}−\mathrm{1}\right)\mathrm{2}\right] \\ $$$$=\mathrm{100} \\ $$$${S}_{{even}} =\mathrm{2}+\mathrm{4}+\mathrm{6}+…+\left[\mathrm{2}+\left(\mathrm{11}−\mathrm{1}\right)\mathrm{2}\right] \\ $$$${S}_{{even}} =\mathrm{2}+\mathrm{4}+\mathrm{6}+…+\mathrm{22} \\ $$$${S}_{{even}} =\mathrm{22}+\mathrm{20}+\mathrm{18}+…+\mathrm{2} \\ $$$${add} \\ $$$$\mathrm{2}{S}_{{even}} =\mathrm{24}+\mathrm{24}+\mathrm{24}…{eleven}\:{times} \\ $$$$\mathrm{2}{S}_{{even}} =\mathrm{24}×\mathrm{11} \\ $$$${S}_{{even}} =\frac{\mathrm{24}×\mathrm{11}}{\mathrm{2}}=\mathrm{132} \\ $$$${or}\:{direct}\:{formula} \\ $$$${S}_{{even}} =\frac{\mathrm{11}}{\mathrm{2}}\left[\mathrm{2}×\mathrm{2}+\left(\mathrm{11}−\mathrm{1}\right)\mathrm{2}\right] \\ $$$${S}_{{even}} =\frac{\mathrm{11}}{\mathrm{2}}\left[\mathrm{24}\right]=\mathrm{132} \\ $$
