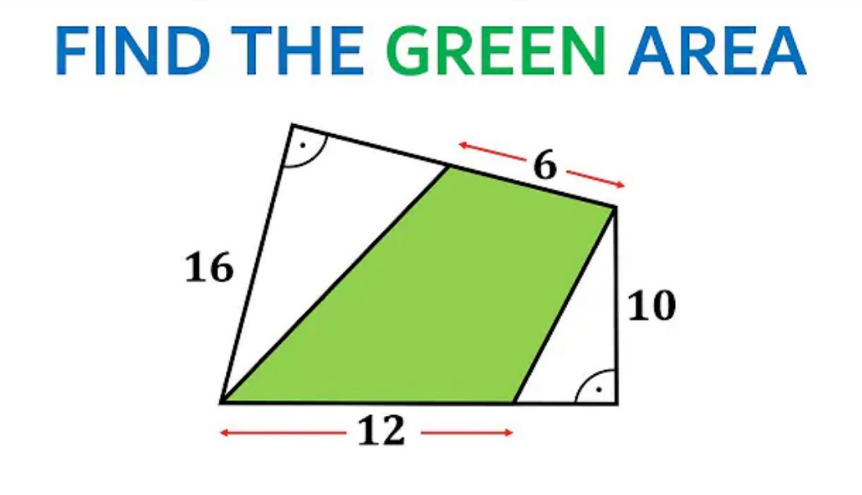
Question Number 206737 by mr W last updated on 23/Apr/24
Commented by A5T last updated on 23/Apr/24
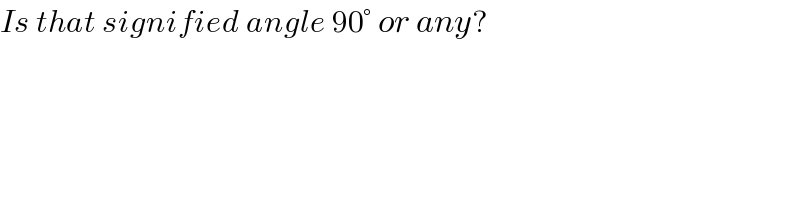
$${Is}\:{that}\:{signified}\:{angle}\:\mathrm{90}°\:{or}\:{any}? \\ $$
Commented by mr W last updated on 23/Apr/24

$$\mathrm{90}° \\ $$
Commented by A5T last updated on 23/Apr/24

$$\mathrm{108}? \\ $$
Commented by mr W last updated on 23/Apr/24

$${right}! \\ $$
Answered by A5T last updated on 23/Apr/24
Commented by A5T last updated on 23/Apr/24
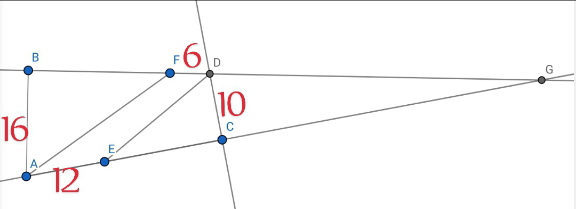
![((DG)/(AG))=((10)/(16))=(5/8); DG=5x;AG=8x ((CG)/(BG))=(5/8); CG=5y;BG=8y 25x^2 =100+25y^2 ⇒x^2 −y^2 =4⇒x=(√(4+y^2 )) EC=8x−12−5y=8(√(4+y^2 ))−5y−12 AC=8(√(4+y^2 ))−5y; BD=8y−5(√(4+y^2 )) BF=8y−5(√(4+y^2 ))−6 [ABDC]=((AB×BD+AC×CD)/2)=39y [BFA]+[DEC]=((AB×BF+EC×DC)/2)=39y−108 ⇒[FAED]=39y−(39y−108)=108](https://www.tinkutara.com/question/Q206744.png)
$$\frac{{DG}}{{AG}}=\frac{\mathrm{10}}{\mathrm{16}}=\frac{\mathrm{5}}{\mathrm{8}};\:{DG}=\mathrm{5}{x};{AG}=\mathrm{8}{x} \\ $$$$\frac{{CG}}{{BG}}=\frac{\mathrm{5}}{\mathrm{8}};\:{CG}=\mathrm{5}{y};{BG}=\mathrm{8}{y} \\ $$$$\mathrm{25}{x}^{\mathrm{2}} =\mathrm{100}+\mathrm{25}{y}^{\mathrm{2}} \Rightarrow{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{4}\Rightarrow{x}=\sqrt{\mathrm{4}+{y}^{\mathrm{2}} } \\ $$$${EC}=\mathrm{8}{x}−\mathrm{12}−\mathrm{5}{y}=\mathrm{8}\sqrt{\mathrm{4}+{y}^{\mathrm{2}} }−\mathrm{5}{y}−\mathrm{12} \\ $$$${AC}=\mathrm{8}\sqrt{\mathrm{4}+{y}^{\mathrm{2}} }−\mathrm{5}{y};\:{BD}=\mathrm{8}{y}−\mathrm{5}\sqrt{\mathrm{4}+{y}^{\mathrm{2}} } \\ $$$${BF}=\mathrm{8}{y}−\mathrm{5}\sqrt{\mathrm{4}+{y}^{\mathrm{2}} }−\mathrm{6} \\ $$$$\left[{ABDC}\right]=\frac{{AB}×{BD}+{AC}×{CD}}{\mathrm{2}}=\mathrm{39}{y} \\ $$$$\left[{BFA}\right]+\left[{DEC}\right]=\frac{{AB}×{BF}+{EC}×{DC}}{\mathrm{2}}=\mathrm{39}{y}−\mathrm{108} \\ $$$$\Rightarrow\left[{FAED}\right]=\mathrm{39}{y}−\left(\mathrm{39}{y}−\mathrm{108}\right)=\mathrm{108} \\ $$
Commented by mr W last updated on 23/Apr/24
��
Answered by mr W last updated on 23/Apr/24
Commented by mr W last updated on 23/Apr/24
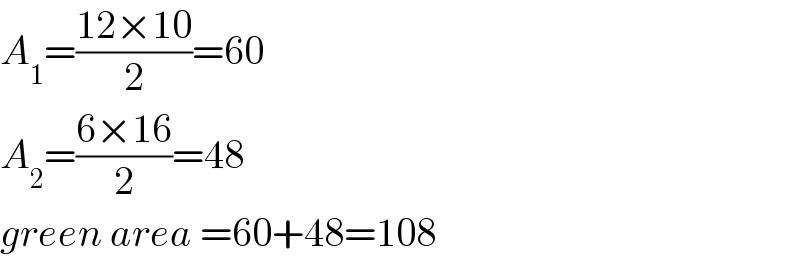
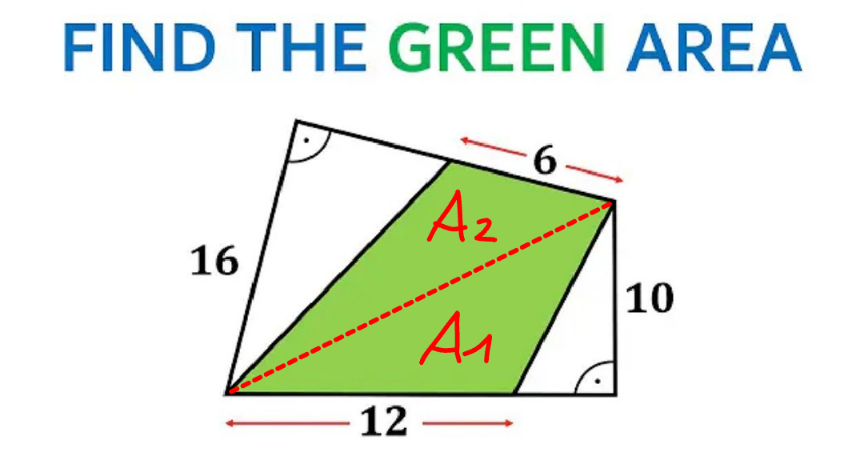
$${A}_{\mathrm{1}} =\frac{\mathrm{12}×\mathrm{10}}{\mathrm{2}}=\mathrm{60} \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{6}×\mathrm{16}}{\mathrm{2}}=\mathrm{48} \\ $$$${green}\:{area}\:=\mathrm{60}+\mathrm{48}=\mathrm{108} \\ $$
