Question Number 144826 by mathdanisur last updated on 29/Jun/21
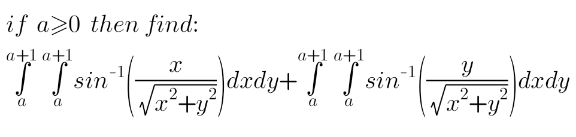
Answered by mindispower last updated on 29/Jun/21
![sin^− (a)+sin^− (b)=u a,b∈[0,1] sin(u)=a(√(1−b^2 ))+b(√(1−a^2 )) u=sin^− (a(√(1−b^2 ))+b(√(1−a^2 ))) a=(x/( (√(x^2 +y^2 )))),b=(y/( (√(x^2 +y^2 )))) sin^− ((x/( (√(x^2 +y^2 )))))+sin^− ((y/( (√(x^2 +y^2 ))))) =sin^− ((x/( (√(x^2 +y^2 )))).(√(1−(y^2 /(x^2 +y^2 ))))+(y/( (√(x^2 +y^2 )))).(√(1−(x^2 /(x^2 +y^2 ))))) =sin^− (((x^2 +y^2 )/(x^2 +y^2 )))=(π/2) ⇔∫_a ^(a+1) ∫_a ^(a+1) (π/2)dxdy=(π/2)](https://www.tinkutara.com/question/Q144867.png)
$${sin}^{−} \left({a}\right)+{sin}^{−} \left({b}\right)={u} \\ $$$${a},{b}\in\left[\mathrm{0},\mathrm{1}\right] \\ $$$${sin}\left({u}\right)={a}\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }+{b}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} } \\ $$$${u}={sin}^{−} \left({a}\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }+{b}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }\right) \\ $$$${a}=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }},{b}=\frac{{y}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }} \\ $$$${sin}^{−} \left(\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\right)+{sin}^{−} \left(\frac{{y}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\right) \\ $$$$={sin}^{−} \left(\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}.\sqrt{\mathrm{1}−\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}+\frac{{y}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}.\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\right) \\ $$$$={sin}^{−} \left(\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\Leftrightarrow\int_{{a}} ^{{a}+\mathrm{1}} \int_{{a}} ^{{a}+\mathrm{1}} \frac{\pi}{\mathrm{2}}{dxdy}=\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Commented by mathdanisur last updated on 29/Jun/21
$${alot}\:{perfect}\:{Sir}\:{thanks} \\ $$
