Question Number 144928 by ArielVyny last updated on 30/Jun/21
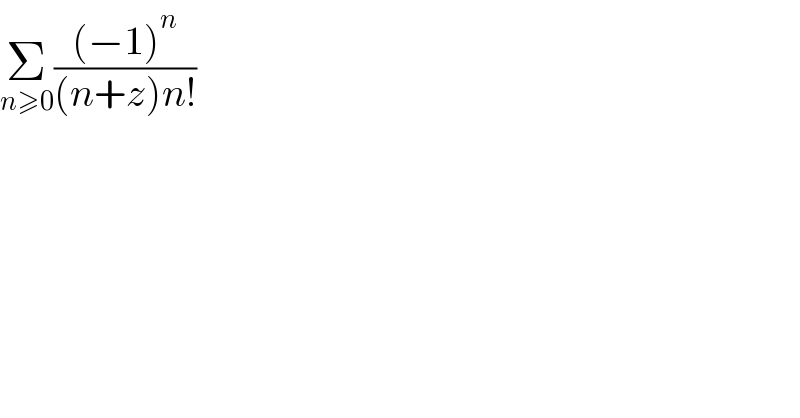
$$\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+{z}\right){n}!} \\ $$
Answered by Dwaipayan Shikari last updated on 01/Jul/21
![∫_0 ^1 Σ_(n≥0) (((−1)^n )/(n!))x^(n+z−1) dx =∫_0 ^1 e^(−x) x^(z−1) dx=[−e^(−x) x^(z−1) ]_0 ^1 +(z−1)∫_0 ^1 e^(−x) x^(z−2) dx I(z−1)=−(1/e)+(z−1)I(z−2) ... Or ∫_0 ^1 e^(−x) x^(z−1) dz=Γ(1,z) (Incomplete Gamma function)](https://www.tinkutara.com/question/Q144953.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}{x}^{{n}+{z}−\mathrm{1}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{x}} {x}^{{z}−\mathrm{1}} {dx}=\left[−{e}^{−{x}} {x}^{{z}−\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} +\left({z}−\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{x}} {x}^{{z}−\mathrm{2}} {dx} \\ $$$${I}\left({z}−\mathrm{1}\right)=−\frac{\mathrm{1}}{{e}}+\left({z}−\mathrm{1}\right){I}\left({z}−\mathrm{2}\right) \\ $$$$…\:{Or}\:\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{x}} {x}^{{z}−\mathrm{1}} {dz}=\Gamma\left(\mathrm{1},{z}\right)\:\:\left({Incomplete}\:{Gamma}\:{function}\right) \\ $$
