Question Number 79607 by sou99 last updated on 26/Jan/20
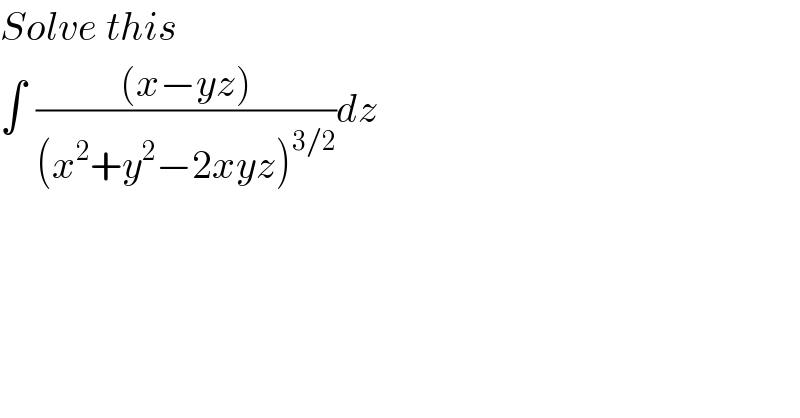
$${Solve}\:{this} \\ $$$$\int_{} \frac{\left({x}−{yz}\right)}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{xyz}\right)^{\mathrm{3}/\mathrm{2}} }{dz} \\ $$$$ \\ $$$$ \\ $$
Commented by MJS last updated on 26/Jan/20
![∫((a+bt)/((c+dt)^(3/2) ))dt= [u=c+dt → dt=(du/d)] =(b/d^2 )∫(du/u^(1/2) )+((ad−bc)/d^2 )∫(du/u^(3/2) )= =((2b)/d^2 )u^(1/2) −((2(ad−bc))/d^2 )u^(−1/2) = =((2(bu−ad+bc))/d^2 (√u))=((2(bdt−ad+2bc))/d^2 (√(c+dt)))= now put a=x, b=−y, c=x^2 +y^2 , d=−2xy, t=z =(((xz−y))/(x^2 (√(x^2 +y^2 −2xyz))))+C](https://www.tinkutara.com/question/Q79620.png)
$$\int\frac{{a}+{bt}}{\left({c}+{dt}\right)^{\mathrm{3}/\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[{u}={c}+{dt}\:\rightarrow\:{dt}=\frac{{du}}{{d}}\right] \\ $$$$=\frac{{b}}{{d}^{\mathrm{2}} }\int\frac{{du}}{{u}^{\mathrm{1}/\mathrm{2}} }+\frac{{ad}−{bc}}{{d}^{\mathrm{2}} }\int\frac{{du}}{{u}^{\mathrm{3}/\mathrm{2}} }= \\ $$$$=\frac{\mathrm{2}{b}}{{d}^{\mathrm{2}} }{u}^{\mathrm{1}/\mathrm{2}} −\frac{\mathrm{2}\left({ad}−{bc}\right)}{{d}^{\mathrm{2}} }{u}^{−\mathrm{1}/\mathrm{2}} = \\ $$$$=\frac{\mathrm{2}\left({bu}−{ad}+{bc}\right)}{{d}^{\mathrm{2}} \sqrt{{u}}}=\frac{\mathrm{2}\left({bdt}−{ad}+\mathrm{2}{bc}\right)}{{d}^{\mathrm{2}} \sqrt{{c}+{dt}}}= \\ $$$$\mathrm{now}\:\mathrm{put} \\ $$$${a}={x},\:{b}=−{y},\:{c}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} ,\:{d}=−\mathrm{2}{xy},\:{t}={z} \\ $$$$=\frac{\left({xz}−{y}\right)}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{xyz}}}+{C} \\ $$
