Question Number 79869 by Henri Boucatchou last updated on 28/Jan/20
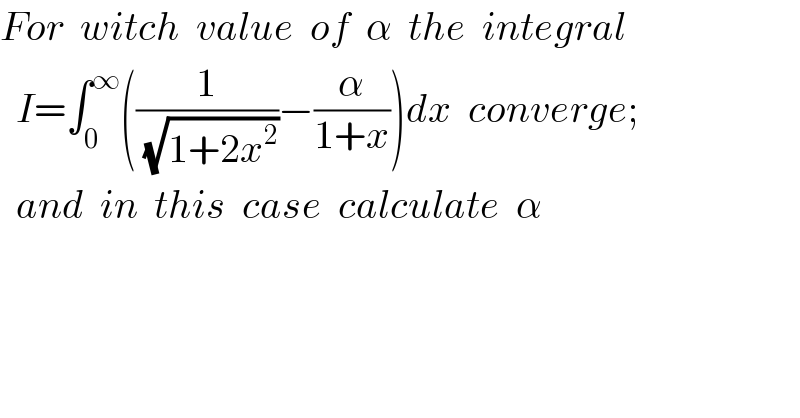
$${For}\:\:{witch}\:\:{value}\:\:{of}\:\:\alpha\:\:{the}\:\:{integral} \\ $$$$\:\:{I}=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }}−\frac{\alpha}{\mathrm{1}+{x}}\right){dx}\:\:{converge}; \\ $$$$\:\:{and}\:\:{in}\:\:{this}\:\:{case}\:\:{calculate}\:\:\alpha \\ $$
Commented by mathmax by abdo last updated on 29/Jan/20
![let a>0 we have I =∫_0 ^a ((1/( (√(1+2x^2 ))))−(α/(1+x)))dx +∫_a ^(+∞) ((1/( (√(1+2x^2 ))))−(α/(1+x)))dx the gunction x→(1/( (√(1+2x^2 ))))−(α/(1+x)) is continue on [0,a] ⇒ integrable on[0,a] ∀α now let look what happend on +∞! we have (1/( (√(1+2x^2 ))))−(α/(1+x)) =(1/(x(√2)((√((1/(2x^2 ))+1))))) −(α/(x(1+(1/x)))) =(1/(x(√2)))(1+(1/(2x^2 )))^(−(1/2)) −(α/(x(1+(1/x)))) ∼(1/(x(√2))){1−(1/(4x^2 ))}−(α/x)(1−(1/x)) ∼(1/x)((1/( (√2)))−α)−(1/(4(√2)x^3 )) +(α/x^2 ) so I converges ⇔(1/( (√2)))−α=0 ⇒α=(1/( (√2))) if α≠(1/( (√2))) this integral diverges!](https://www.tinkutara.com/question/Q79985.png)
$${let}\:{a}>\mathrm{0}\:\:{we}\:{have}\:{I}\:=\int_{\mathrm{0}} ^{{a}} \:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }}−\frac{\alpha}{\mathrm{1}+{x}}\right){dx}\:+\int_{{a}} ^{+\infty} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }}−\frac{\alpha}{\mathrm{1}+{x}}\right){dx} \\ $$$${the}\:{gunction}\:{x}\rightarrow\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }}−\frac{\alpha}{\mathrm{1}+{x}}\:{is}\:{continue}\:{on}\:\left[\mathrm{0},{a}\right]\:\Rightarrow \\ $$$${integrable}\:{on}\left[\mathrm{0},{a}\right]\:\forall\alpha\:\:{now}\:{let}\:{look}\:{what}\:{happend}\:{on}\:+\infty! \\ $$$${we}\:{have}\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} }}−\frac{\alpha}{\mathrm{1}+{x}}\:=\frac{\mathrm{1}}{{x}\sqrt{\mathrm{2}}\left(\sqrt{\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{1}}\right)}\:−\frac{\alpha}{{x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)} \\ $$$$=\frac{\mathrm{1}}{{x}\sqrt{\mathrm{2}}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:−\frac{\alpha}{{x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)}\:\sim\frac{\mathrm{1}}{{x}\sqrt{\mathrm{2}}}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} }\right\}−\frac{\alpha}{{x}}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right) \\ $$$$\sim\frac{\mathrm{1}}{{x}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\alpha\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}{x}^{\mathrm{3}} }\:+\frac{\alpha}{{x}^{\mathrm{2}} }\:\:\:{so}\:{I}\:{converges}\:\Leftrightarrow\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\alpha=\mathrm{0}\:\Rightarrow\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${if}\:\alpha\neq\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{this}\:{integral}\:{diverges}! \\ $$
