Question Number 145646 by physicstutes last updated on 06/Jul/21
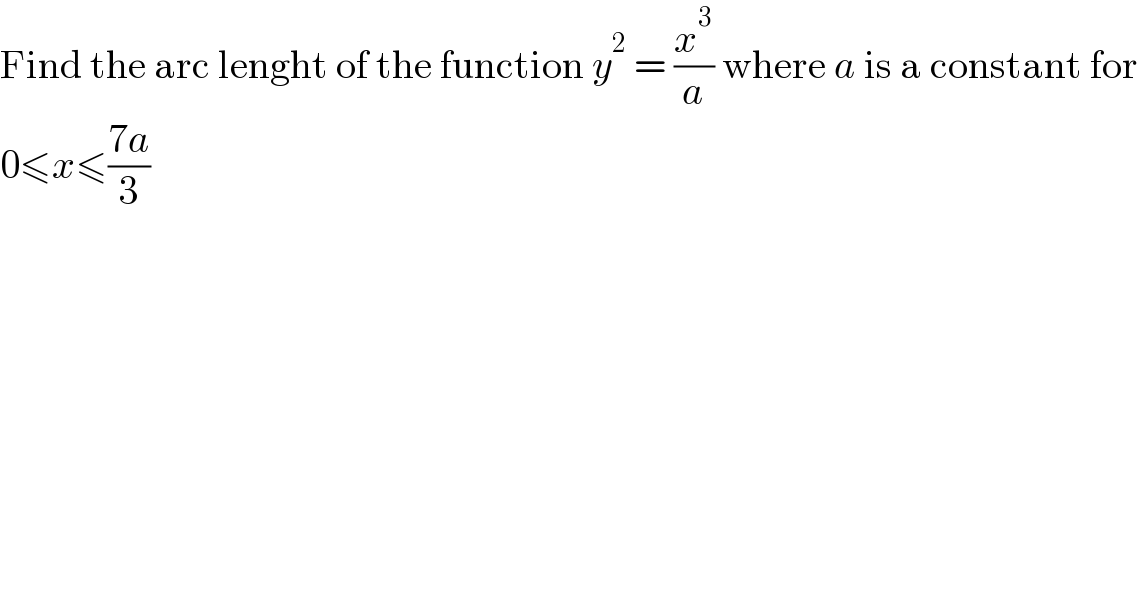
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{arc}\:\mathrm{lenght}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:{y}^{\mathrm{2}} \:=\:\frac{{x}^{\mathrm{3}} }{{a}}\:\mathrm{where}\:{a}\:\mathrm{is}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{for} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\frac{\mathrm{7}{a}}{\mathrm{3}} \\ $$
Answered by Olaf_Thorendsen last updated on 06/Jul/21
![y^2 = (x^3 /a) y = (x^(3/2) /( (√a))) y′ = ((3(√x))/( 2(√a))) L = ∫_0 ^((7a)/3) (√(1+y′^2 ))dx L = ∫_0 ^((7a)/3) (√(1+((9x)/(4a))))dx L = ((8a)/(27))[(1+((9x)/(4a)))^(3/2) ]_0 ^((7a)/3) L = ((8a)/(27))(((25a)/4)−1) = ((2a)/(27))(25a−4)](https://www.tinkutara.com/question/Q145649.png)
$${y}^{\mathrm{2}} \:=\:\frac{{x}^{\mathrm{3}} }{{a}} \\ $$$${y}\:=\:\frac{{x}^{\mathrm{3}/\mathrm{2}} }{\:\sqrt{{a}}} \\ $$$${y}'\:=\:\frac{\mathrm{3}\sqrt{{x}}}{\:\mathrm{2}\sqrt{{a}}} \\ $$$$\mathrm{L}\:=\:\int_{\mathrm{0}} ^{\frac{\mathrm{7}{a}}{\mathrm{3}}} \sqrt{\mathrm{1}+{y}'^{\mathrm{2}} }{dx} \\ $$$$\mathrm{L}\:=\:\int_{\mathrm{0}} ^{\frac{\mathrm{7}{a}}{\mathrm{3}}} \sqrt{\mathrm{1}+\frac{\mathrm{9}{x}}{\mathrm{4}{a}}}{dx} \\ $$$$\mathrm{L}\:=\:\frac{\mathrm{8}{a}}{\mathrm{27}}\left[\left(\mathrm{1}+\frac{\mathrm{9}{x}}{\mathrm{4}{a}}\right)^{\mathrm{3}/\mathrm{2}} \right]_{\mathrm{0}} ^{\frac{\mathrm{7}{a}}{\mathrm{3}}} \\ $$$$\mathrm{L}\:=\:\frac{\mathrm{8}{a}}{\mathrm{27}}\left(\frac{\mathrm{25}{a}}{\mathrm{4}}−\mathrm{1}\right)\:=\:\frac{\mathrm{2}{a}}{\mathrm{27}}\left(\mathrm{25}{a}−\mathrm{4}\right) \\ $$
Commented by physicstutes last updated on 06/Jul/21

$$\mathrm{I}\:\mathrm{appreciate} \\ $$
Commented by gsk2684 last updated on 07/Jul/21
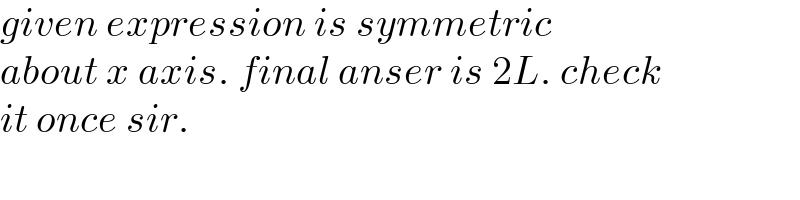
$${given}\:{expression}\:{is}\:{symmetric}\: \\ $$$${about}\:{x}\:{axis}.\:{final}\:{anser}\:{is}\:\mathrm{2}{L}.\:{check}\: \\ $$$${it}\:{once}\:{sir}. \\ $$
