Question Number 81829 by aseer imad last updated on 15/Feb/20
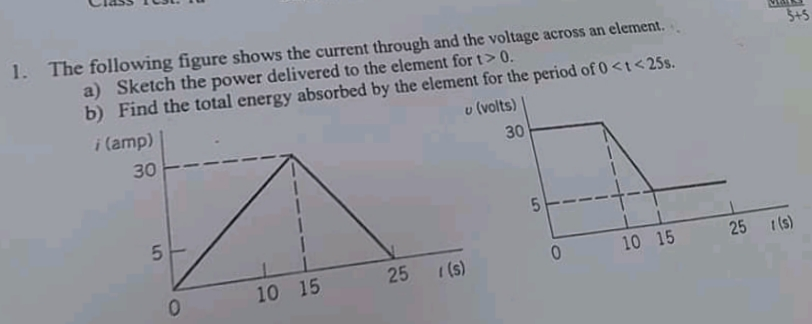
Commented by aseer imad last updated on 15/Feb/20

$${pls}\:{help}… \\ $$
Commented by aseer imad last updated on 15/Feb/20

$${pls}\:{help}… \\ $$
Answered by TANMAY PANACEA last updated on 15/Feb/20
![dw=vdq (dw/dt)=v×(dq/dt)=vi=power dw=(v)idt=vidt energy=∫_(0 ) ^(10) vidt+∫_(10) ^(15) vidt+∫_(15) ^(25) vidt compare with y=mx i=(((30)/(15)))t=2t [when 15≥t≥0] eqn of st line joining (25,0) and(15,30) (t,i) t=time i=current t→x i→y →(y−y_1 )=((y_2 −y_1 )/(x_2 −x_1 ))(x−x_1 ) i−0=((30−0)/(15−25))(t−25) i=−3(t−25) i=−3t+75 relation between v and t when15> t>10 (t,v)→(x,y) (10,30) and(15,5) (v−30)=((5−30)/(15−10))(i−10) v−30=((−25)/5)(i−10) v=30−5i+50 v=80−5i so complte answer ∫_0 ^(10) vidt+∫_(10) ^(15) vidt+∫_(15) ^(25) vidt =∫_0 ^(10) 30idt+∫_(10) ^(15) (80−5i)idt+∫_(15) ^(25) 5idt pls check upto this ∫_0 ^(10) 30(2t)dt+∫_(10) ^(15) (80−5×2t)2tdt+∫_(15) ^(25) 5×(−3t+75)dt i=2t for time interval t 0 to 10 sec i=2t for time interval 10 to 15 sec i=(−3t+75) for time interval 15 to 25 now pls complete the rest by you](https://www.tinkutara.com/question/Q81832.png)
$${dw}={vdq} \\ $$$$\frac{{dw}}{{dt}}={v}×\frac{{dq}}{{dt}}={vi}={power} \\ $$$${dw}=\left({v}\right){idt}={vidt} \\ $$$${energy}=\int_{\mathrm{0}\:} ^{\mathrm{10}} {vidt}+\int_{\mathrm{10}} ^{\mathrm{15}} {vidt}+\int_{\mathrm{15}} ^{\mathrm{25}} {vidt} \\ $$$${compare}\:{with}\:{y}={mx} \\ $$$${i}=\left(\frac{\mathrm{30}}{\mathrm{15}}\right){t}=\mathrm{2}{t}\:\:\left[{when}\:\mathrm{15}\geqslant{t}\geqslant\mathrm{0}\right] \\ $$$${eqn}\:{of}\:{st}\:{line}\:{joining}\:\left(\mathrm{25},\mathrm{0}\right)\:{and}\left(\mathrm{15},\mathrm{30}\right)\:\:\left({t},{i}\right) \\ $$$${t}={time}\:\:{i}={current} \\ $$$${t}\rightarrow{x}\:\:\:\:\:{i}\rightarrow{y}\:\:\rightarrow\left({y}−{y}_{\mathrm{1}} \right)=\frac{{y}_{\mathrm{2}} −{y}_{\mathrm{1}} }{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }\left({x}−{x}_{\mathrm{1}} \right) \\ $$$${i}−\mathrm{0}=\frac{\mathrm{30}−\mathrm{0}}{\mathrm{15}−\mathrm{25}}\left({t}−\mathrm{25}\right)\:\:\:\:{i}=−\mathrm{3}\left({t}−\mathrm{25}\right) \\ $$$${i}=−\mathrm{3}{t}+\mathrm{75} \\ $$$$ \\ $$$${relation}\:{between}\:{v}\:{and}\:{t}\:{when}\mathrm{15}>\:{t}>\mathrm{10} \\ $$$$\left({t},{v}\right)\rightarrow\left({x},{y}\right)\:\:\left(\mathrm{10},\mathrm{30}\right)\:{and}\left(\mathrm{15},\mathrm{5}\right) \\ $$$$\left({v}−\mathrm{30}\right)=\frac{\mathrm{5}−\mathrm{30}}{\mathrm{15}−\mathrm{10}}\left({i}−\mathrm{10}\right) \\ $$$${v}−\mathrm{30}=\frac{−\mathrm{25}}{\mathrm{5}}\left({i}−\mathrm{10}\right) \\ $$$${v}=\mathrm{30}−\mathrm{5}{i}+\mathrm{50} \\ $$$${v}=\mathrm{80}−\mathrm{5}{i} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{complte}}\:\boldsymbol{{answer}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{10}} {vidt}+\int_{\mathrm{10}} ^{\mathrm{15}} {vidt}+\int_{\mathrm{15}} ^{\mathrm{25}} {vidt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{10}} \mathrm{30}{idt}+\int_{\mathrm{10}} ^{\mathrm{15}} \left(\mathrm{80}−\mathrm{5}{i}\right){idt}+\int_{\mathrm{15}} ^{\mathrm{25}} \mathrm{5}{idt} \\ $$$$\boldsymbol{{pls}}\:\boldsymbol{{check}}\:\boldsymbol{{upto}}\:\boldsymbol{{this}}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{10}} \mathrm{30}\left(\mathrm{2}{t}\right){dt}+\int_{\mathrm{10}} ^{\mathrm{15}} \left(\mathrm{80}−\mathrm{5}×\mathrm{2}{t}\right)\mathrm{2}{tdt}+\int_{\mathrm{15}} ^{\mathrm{25}} \mathrm{5}×\left(−\mathrm{3}{t}+\mathrm{75}\right){dt} \\ $$$${i}=\mathrm{2}{t}\:\:{for}\:{time}\:{interval}\:{t}\:\:\mathrm{0}\:{to}\:\mathrm{10}\:{sec} \\ $$$${i}=\mathrm{2}{t}\:\:{for}\:{time}\:{interval}\:\:\:\mathrm{10}\:{to}\:\mathrm{15}\:{sec} \\ $$$${i}=\left(−\mathrm{3}{t}+\mathrm{75}\right)\:\:{for}\:{time}\:{interval}\:\:\mathrm{15}\:{to}\:\mathrm{25} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{pls}}\:\boldsymbol{{complete}}\:\boldsymbol{{the}}\:\boldsymbol{{rest}}\:\boldsymbol{{by}}\:\boldsymbol{{you}} \\ $$
