Question Number 81944 by M±th+et£s last updated on 16/Feb/20
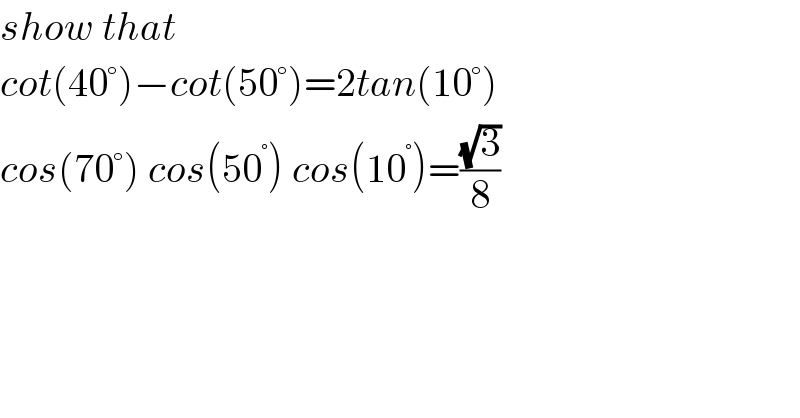
$${show}\:{that}\: \\ $$$${cot}\left(\mathrm{40}°\right)−{cot}\left(\mathrm{50}°\right)=\mathrm{2}{tan}\left(\mathrm{10}°\right) \\ $$$${cos}\left(\mathrm{70}°\right)\:{cos}\left(\mathrm{50}^{°} \right)\:{cos}\left(\mathrm{10}^{°} \right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{8}} \\ $$
Answered by TANMAY PANACEA last updated on 16/Feb/20
![tan10^o =tan(50^o −40^o ) =((tan50−tan40)/(1+tan50.tan40)) =(((1/(cot50))−(1/(cot40)))/(1+1)) [tan50×tan40=tan50×cot50=1] 2tan10=((cot40−co50)/(cot50cot40)) [cot50×cot40=1] so cot4o−cot50=2tan10 proved](https://www.tinkutara.com/question/Q81945.png)
$${tan}\mathrm{10}^{{o}} ={tan}\left(\mathrm{50}^{{o}} −\mathrm{40}^{{o}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{tan}\mathrm{50}−{tan}\mathrm{40}}{\mathrm{1}+{tan}\mathrm{50}.{tan}\mathrm{40}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\frac{\mathrm{1}}{{cot}\mathrm{50}}−\frac{\mathrm{1}}{{cot}\mathrm{40}}}{\mathrm{1}+\mathrm{1}}\:\:\:\left[{tan}\mathrm{50}×{tan}\mathrm{40}={tan}\mathrm{50}×{cot}\mathrm{50}=\mathrm{1}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2}{tan}\mathrm{10}=\frac{{cot}\mathrm{40}−{co}\mathrm{50}}{{cot}\mathrm{50}{cot}\mathrm{40}}\:\:\:\:\:\left[{cot}\mathrm{50}×{cot}\mathrm{40}=\mathrm{1}\right] \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{cot}}\mathrm{4}\boldsymbol{{o}}−\boldsymbol{{cot}}\mathrm{50}=\mathrm{2}\boldsymbol{{tan}}\mathrm{10}\:\boldsymbol{{proved}} \\ $$
Answered by TANMAY PANACEA last updated on 16/Feb/20
![cos(60+10)cos(60−10)cos10 =(cos60cos10−sin60sin10)(cos60cos10+sin60sin10)cos10 =[((1/(2 ))cos10)^2 −(((√3)/2)sin10)^2 ]×cos10 =((cos^2 10−3sin^2 10)/4)×cos10 =((cos^3 10−3(1−cos^2 10)cos10)/4) =((4cos^3 10−3cos10)/4) =((cos(3×10))/4)=((√3)/(2×4))=((√3)/8)](https://www.tinkutara.com/question/Q81946.png)
$${cos}\left(\mathrm{60}+\mathrm{10}\right){cos}\left(\mathrm{60}−\mathrm{10}\right){cos}\mathrm{10} \\ $$$$=\left({cos}\mathrm{60}{cos}\mathrm{10}−{sin}\mathrm{60}{sin}\mathrm{10}\right)\left({cos}\mathrm{60}{cos}\mathrm{10}+{sin}\mathrm{60}{sin}\mathrm{10}\right){cos}\mathrm{10} \\ $$$$=\left[\left(\frac{\mathrm{1}}{\mathrm{2}\:}{cos}\mathrm{10}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sin}\mathrm{10}\right)^{\mathrm{2}} \right]×{cos}\mathrm{10} \\ $$$$=\frac{{cos}^{\mathrm{2}} \mathrm{10}−\mathrm{3}{sin}^{\mathrm{2}} \mathrm{10}}{\mathrm{4}}×{cos}\mathrm{10} \\ $$$$=\frac{{cos}^{\mathrm{3}} \mathrm{10}−\mathrm{3}\left(\mathrm{1}−{cos}^{\mathrm{2}} \mathrm{10}\right){cos}\mathrm{10}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{4}{cos}^{\mathrm{3}} \mathrm{10}−\mathrm{3}{cos}\mathrm{10}}{\mathrm{4}} \\ $$$$=\frac{{cos}\left(\mathrm{3}×\mathrm{10}\right)}{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}×\mathrm{4}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{8}} \\ $$
Commented by M±th+et£s last updated on 16/Feb/20

$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by TANMAY PANACEA last updated on 16/Feb/20

$${god}\:{bless}\:{to}\:{all}\:{of}\:{us} \\ $$
