Menu Close

soit-0-pi-determiner-1-le-module-et-l-argument-de-a-1-e-i-b-1-e-i-2-deduire-le-module-et-l-argument-de-a-1-e-i-1-e-i-b-1-e-i-1-e-i-rochinel930-gmail-c-

Tinku Tara 0 Comments
Pin




Question Number 81954 by Cmr 237 last updated on 16/Feb/20
soit α∈]0;π[. determiner: 1)le module et l′argument de: a)1−e^(iα) ,b)1+e^(i𝛂) 2)deduire le module et l′argument de a) ((1−e^(iα) )/(1+e^(iα) )), b)(1−e^(iα) )(1+e^(iα) ) rochinel930@gmail.c
$$\left.\:{soit}\:\alpha\in\right]\mathrm{0};\pi\left[.\:{determiner}:\right. \\ $$$$\left.\mathrm{1}\right){le}\:{module}\:{et}\:{l}'{argument}\:{de}: \\ $$$$\left.\boldsymbol{{a}}\left.\right)\mathrm{1}−\boldsymbol{{e}}^{\boldsymbol{{i}}\alpha} ,\boldsymbol{{b}}\right)\mathrm{1}+\boldsymbol{{e}}^{\boldsymbol{{i}\alpha}} \\ $$$$\left.\mathrm{2}\right)\boldsymbol{{deduire}}\:\boldsymbol{{le}}\:\boldsymbol{{module}}\:\boldsymbol{{et}}\:\boldsymbol{{l}}'\boldsymbol{{argument}}\:\boldsymbol{{de}} \\ $$$$\left.\:\left.\boldsymbol{{a}}\right)\:\frac{\mathrm{1}−\boldsymbol{{e}}^{\boldsymbol{{i}}\alpha} }{\mathrm{1}+{e}^{{i}\alpha} },\:{b}\right)\left(\mathrm{1}−{e}^{{i}\alpha} \right)\left(\mathrm{1}+{e}^{{i}\alpha} \right) \\ $$$$\:\boldsymbol{{rochinel}}\mathrm{930}@{gmail}.\boldsymbol{{c}} \\ $$
Commented by abdomathmax last updated on 16/Feb/20
z=1−e^(iα) =1−cosα−isinα =2sin^2 ((α/2))−2isin((α/2))cos((α/2)) =2sin((α/2))(sin((α/2))−icos((α/2))) 0<(α/2)<(π/2) ⇒sin((α/2))>0 ⇒z=2sin((α/2)){cos((π/2)−(α/2))−isin((π/2)−(α/2))} =2sin((α/2)){cos(((α−π)/2))+isin(((α−π)/2))} ⇒ ∣z∣=2sin((α/2)) and arg(z)=((α−π)/2) [2π]
$${z}=\mathrm{1}−{e}^{{i}\alpha} \:=\mathrm{1}−{cos}\alpha−{isin}\alpha\:=\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)−\mathrm{2}{isin}\left(\frac{\alpha}{\mathrm{2}}\right){cos}\left(\frac{\alpha}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\left({sin}\left(\frac{\alpha}{\mathrm{2}}\right)−{icos}\left(\frac{\alpha}{\mathrm{2}}\right)\right) \\ $$$$\mathrm{0}<\frac{\alpha}{\mathrm{2}}<\frac{\pi}{\mathrm{2}}\:\Rightarrow{sin}\left(\frac{\alpha}{\mathrm{2}}\right)>\mathrm{0}\:\Rightarrow{z}=\mathrm{2}{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\left\{{cos}\left(\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}\right)−{isin}\left(\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}\right)\right\} \\ $$$$=\mathrm{2}{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\left\{{cos}\left(\frac{\alpha−\pi}{\mathrm{2}}\right)+{isin}\left(\frac{\alpha−\pi}{\mathrm{2}}\right)\right\}\:\Rightarrow \\ $$$$\mid{z}\mid=\mathrm{2}{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\:{and}\:{arg}\left({z}\right)=\frac{\alpha−\pi}{\mathrm{2}}\:\left[\mathrm{2}\pi\right] \\ $$
Commented by abdomathmax last updated on 16/Feb/20
Z=1+e^(iα) ⇒Z=1+cosα +isinα =2cos^2 ((α/2))+2isin((α/2))cos((α/2)) =2cos((α/2)){cos((α/2))+isin((α/2))} cos((α/2))>0 due to 0<α<π ⇒∣Z∣=2cos((α/2))and argZ=(α/2)[2π]
$${Z}=\mathrm{1}+{e}^{{i}\alpha} \:\Rightarrow{Z}=\mathrm{1}+{cos}\alpha\:+{isin}\alpha \\ $$$$=\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)+\mathrm{2}{isin}\left(\frac{\alpha}{\mathrm{2}}\right){cos}\left(\frac{\alpha}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{cos}\left(\frac{\alpha}{\mathrm{2}}\right)\left\{{cos}\left(\frac{\alpha}{\mathrm{2}}\right)+{isin}\left(\frac{\alpha}{\mathrm{2}}\right)\right\} \\ $$$${cos}\left(\frac{\alpha}{\mathrm{2}}\right)>\mathrm{0}\:{due}\:{to}\:\mathrm{0}<\alpha<\pi\:\Rightarrow\mid{Z}\mid=\mathrm{2}{cos}\left(\frac{\alpha}{\mathrm{2}}\right){and} \\ $$$${argZ}=\frac{\alpha}{\mathrm{2}}\left[\mathrm{2}\pi\right] \\ $$
Commented by abdomathmax last updated on 16/Feb/20
∣((1−e^(iα) )/(1+e^(iα) ))∣ =((∣1−e^(iα) ∣)/(∣1+e^(iα) ∣)) =((2sin((α/2)))/(2cos((α/2))))=tan((α/2)) and arg(((1−e^(iα) )/(1+e^(iα) )))=arg(1−e^(iα) )−arg(1+e^(iα) ) [2π] =((α−π)/2)−(α/2)[2π] =−(π/2)[2π]
$$\mid\frac{\mathrm{1}−{e}^{{i}\alpha} }{\mathrm{1}+{e}^{{i}\alpha} }\mid\:=\frac{\mid\mathrm{1}−{e}^{{i}\alpha} \mid}{\mid\mathrm{1}+{e}^{{i}\alpha} \mid}\:=\frac{\mathrm{2}{sin}\left(\frac{\alpha}{\mathrm{2}}\right)}{\mathrm{2}{cos}\left(\frac{\alpha}{\mathrm{2}}\right)}={tan}\left(\frac{\alpha}{\mathrm{2}}\right)\:{and} \\ $$$${arg}\left(\frac{\mathrm{1}−{e}^{{i}\alpha} }{\mathrm{1}+{e}^{{i}\alpha} }\right)={arg}\left(\mathrm{1}−{e}^{{i}\alpha} \right)−{arg}\left(\mathrm{1}+{e}^{{i}\alpha} \right)\:\left[\mathrm{2}\pi\right] \\ $$$$=\frac{\alpha−\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}\left[\mathrm{2}\pi\right]\:=−\frac{\pi}{\mathrm{2}}\left[\mathrm{2}\pi\right] \\ $$
Commented by abdomathmax last updated on 16/Feb/20
∣(1−e^(iα) )(1+e^(iα) )∣=2sin((α/2))×2cos((α/2)) =2sin(α) and arg{(1−e^(iα) )(1+e^(iα) )} =arg(1−e^(iα) ) +arg(1+e^(iα) )[2π] =((α−π)/2) +(α/2) [2π] =α−(π/2)
$$\mid\left(\mathrm{1}−{e}^{{i}\alpha} \right)\left(\mathrm{1}+{e}^{{i}\alpha} \right)\mid=\mathrm{2}{sin}\left(\frac{\alpha}{\mathrm{2}}\right)×\mathrm{2}{cos}\left(\frac{\alpha}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{sin}\left(\alpha\right)\:{and}\:{arg}\left\{\left(\mathrm{1}−{e}^{{i}\alpha} \right)\left(\mathrm{1}+{e}^{{i}\alpha} \right)\right\} \\ $$$$={arg}\left(\mathrm{1}−{e}^{{i}\alpha} \right)\:+{arg}\left(\mathrm{1}+{e}^{{i}\alpha} \right)\left[\mathrm{2}\pi\right] \\ $$$$=\frac{\alpha−\pi}{\mathrm{2}}\:+\frac{\alpha}{\mathrm{2}}\:\left[\mathrm{2}\pi\right]\:=\alpha−\frac{\pi}{\mathrm{2}} \\ $$
Commented by Cmr 237 last updated on 16/Feb/20
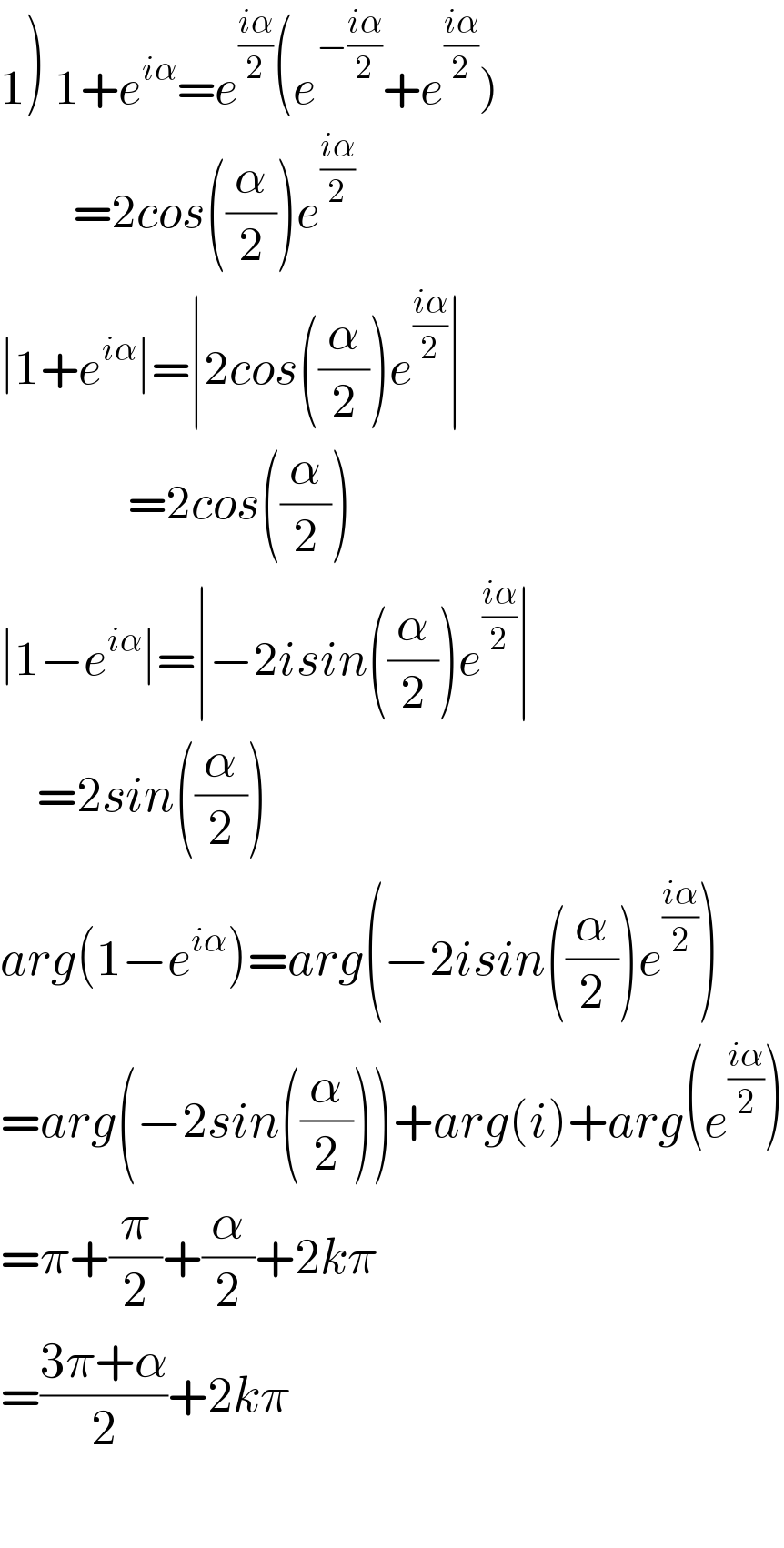
1) 1+e^(iα) =e^((iα)/2) (e^(−((iα)/2)) +e^((iα)/2) ) =2cos((α/2))e^((iα)/2) ∣1+e^(iα) ∣=∣2cos((α/2))e^((iα)/2) ∣ =2cos((α/2)) ∣1−e^(iα) ∣=∣−2isin((α/2))e^((iα)/2) ∣ =2sin((α/2)) arg(1−e^(iα) )=arg(−2isin((α/2))e^((iα)/2) ) =arg(−2sin((α/2)))+arg(i)+arg(e^((iα)/2) ) =π+(π/2)+(α/2)+2kπ =((3π+α)/2)+2kπ
$$\left.\mathrm{1}\right)\:\mathrm{1}+{e}^{{i}\alpha} ={e}^{\frac{{i}\alpha}{\mathrm{2}}} \left({e}^{−\frac{{i}\alpha}{\mathrm{2}}} +{e}^{\frac{{i}\alpha}{\mathrm{2}}} \right)\:\: \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{2}{cos}\left(\frac{\alpha}{\mathrm{2}}\right){e}^{\frac{{i}\alpha}{\mathrm{2}}} \: \\ $$$$\mid\mathrm{1}+{e}^{{i}\alpha} \mid=\mid\mathrm{2}{cos}\left(\frac{\alpha}{\mathrm{2}}\right){e}^{\frac{{i}\alpha}{\mathrm{2}}} \mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{cos}\left(\frac{\alpha}{\mathrm{2}}\right) \\ $$$$\mid\mathrm{1}−{e}^{{i}\alpha} \mid=\mid−\mathrm{2}{isin}\left(\frac{\alpha}{\mathrm{2}}\right){e}^{\frac{{i}\alpha}{\mathrm{2}}} \mid \\ $$$$\:\:\:\:=\mathrm{2}{sin}\left(\frac{\alpha}{\mathrm{2}}\right) \\ $$$${arg}\left(\mathrm{1}−{e}^{{i}\alpha} \right)={arg}\left(−\mathrm{2}{isin}\left(\frac{\alpha}{\mathrm{2}}\right){e}^{\frac{{i}\alpha}{\mathrm{2}}} \right) \\ $$$$={arg}\left(−\mathrm{2}{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\right)+{arg}\left({i}\right)+{arg}\left({e}^{\frac{{i}\alpha}{\mathrm{2}}} \right) \\ $$$$=\pi+\frac{\pi}{\mathrm{2}}+\frac{\alpha}{\mathrm{2}}+\mathrm{2}{k}\pi \\ $$$$=\frac{\mathrm{3}\pi+\alpha}{\mathrm{2}}+\mathrm{2}{k}\pi \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 16/Feb/20
((3π+α)/2) +2kπ =2π−(π/2)+(α/2) +2kπ =((α−π)/2)[2π]
$$\frac{\mathrm{3}\pi+\alpha}{\mathrm{2}}\:+\mathrm{2}{k}\pi\:=\mathrm{2}\pi−\frac{\pi}{\mathrm{2}}+\frac{\alpha}{\mathrm{2}}\:+\mathrm{2}{k}\pi\:=\frac{\alpha−\pi}{\mathrm{2}}\left[\mathrm{2}\pi\right] \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *