Question Number 147539 by alcohol last updated on 21/Jul/21
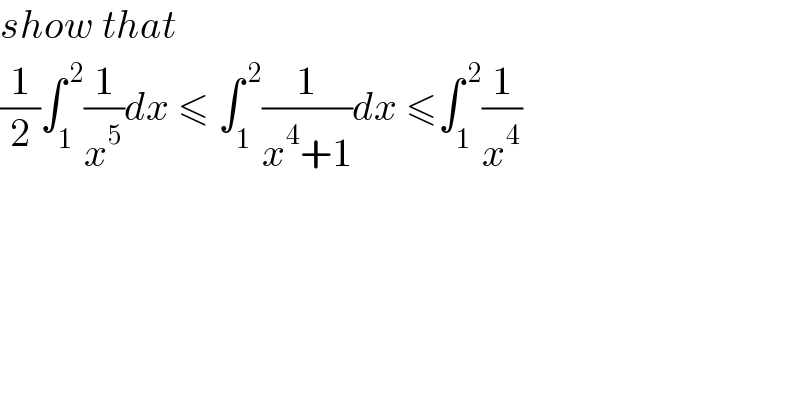
$${show}\:{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{{x}^{\mathrm{5}} }{dx}\:\leqslant\:\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{1}}{dx}\:\leqslant\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{{x}^{\mathrm{4}} } \\ $$
Answered by puissant last updated on 21/Jul/21
![∀ x∈[1;2], x^4 ≤x^4 +1≤2x^5 ⇒ (1/(2x^5 ))≤(1/(x^4 +1))≤(1/x^4 ) ⇒(1/2)∫_1 ^2 (1/x^5 )dx≤∫_1 ^( 2) (1/(x^4 +1))≤∫_1 ^( 2) (1/x^4 )..](https://www.tinkutara.com/question/Q147544.png)
$$\forall\:\mathrm{x}\in\left[\mathrm{1};\mathrm{2}\right], \\ $$$$\mathrm{x}^{\mathrm{4}} \leqslant\mathrm{x}^{\mathrm{4}} +\mathrm{1}\leqslant\mathrm{2x}^{\mathrm{5}} \:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{5}} }\leqslant\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}\leqslant\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{x}^{\mathrm{5}} }\mathrm{dx}\leqslant\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}\leqslant\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }.. \\ $$
Answered by puissant last updated on 21/Jul/21

$$\mathrm{polytech}\:\mathrm{yaound}\acute {\mathrm{e}}\:\mathrm{premi}\grave {\mathrm{e}re}\:\acute {\mathrm{e}preuve}.. \\ $$
