Question Number 82446 by M±th+et£s last updated on 21/Feb/20
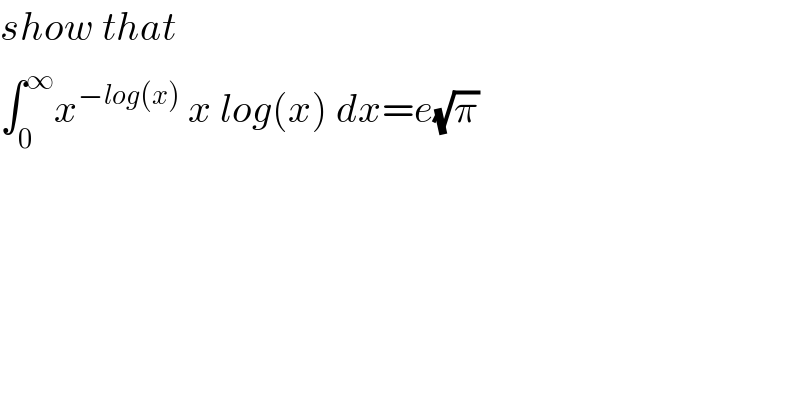
$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}^{−{log}\left({x}\right)} \:{x}\:{log}\left({x}\right)\:{dx}={e}\sqrt{\pi} \\ $$
Commented by abdomathmax last updated on 21/Feb/20
![changement logx=t give x=e^t ⇒ I= ∫_(−∞) ^(+∞) (e^t )^(−t) e^t t e^t dt =∫_(−∞) ^(+∞) t e^(−t^2 +2t) dt =∫_(−∞) ^(+∞) t e^(−(t^2 −2t +1−1)) dt =∫_(−∞) ^(+∞) t e^(−(t−1)^2 +1) dt =_(t−1=u) e∫_(−∞) ^(+∞) (u+1)e^(−u^2 ) du but ∫_(−∞) ^(+∞) (u+1)e^(−u^2 ) du =∫_(−∞) ^(+∞) u e^(−u^2 ) du +∫_(−∞) ^(+∞) e^(−u^2 ) du =[−(1/2)e^(−u^2 ) ]_(−∞) ^(+∞) +(√π)=0+(√π) ⇒ I =e(√π)](https://www.tinkutara.com/question/Q82473.png)
$${changement}\:{logx}={t}\:{give}\:{x}={e}^{{t}} \:\Rightarrow \\ $$$${I}=\:\int_{−\infty} ^{+\infty} \:\left({e}^{{t}} \right)^{−{t}} {e}^{{t}} {t}\:{e}^{{t}} \:{dt} \\ $$$$=\int_{−\infty} ^{+\infty} {t}\:{e}^{−{t}^{\mathrm{2}} +\mathrm{2}{t}} \:{dt}\:\:=\int_{−\infty} ^{+\infty} \:{t}\:{e}^{−\left({t}^{\mathrm{2}} −\mathrm{2}{t}\:+\mathrm{1}−\mathrm{1}\right)} {dt} \\ $$$$=\int_{−\infty} ^{+\infty} \:{t}\:{e}^{−\left({t}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}} \:{dt}\:=_{{t}−\mathrm{1}={u}} \:\:{e}\int_{−\infty} ^{+\infty} \left({u}+\mathrm{1}\right){e}^{−{u}^{\mathrm{2}} } {du} \\ $$$${but}\:\:\int_{−\infty} ^{+\infty} \left({u}+\mathrm{1}\right){e}^{−{u}^{\mathrm{2}} } {du} \\ $$$$=\int_{−\infty} ^{+\infty} \:{u}\:{e}^{−{u}^{\mathrm{2}} } {du}\:+\int_{−\infty} ^{+\infty} \:{e}^{−{u}^{\mathrm{2}} } {du} \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−{u}^{\mathrm{2}} } \right]_{−\infty} ^{+\infty} \:+\sqrt{\pi}=\mathrm{0}+\sqrt{\pi}\:\Rightarrow \\ $$$${I}\:={e}\sqrt{\pi} \\ $$
Commented by M±th+et£s last updated on 21/Feb/20

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 21/Feb/20
$${you}\:{are}\:{welcome}. \\ $$
