Question Number 82570 by jagoll last updated on 22/Feb/20
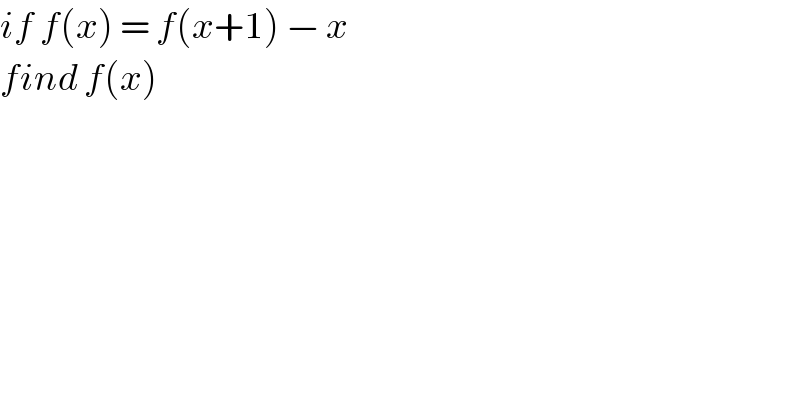
$${if}\:{f}\left({x}\right)\:=\:{f}\left({x}+\mathrm{1}\right)\:−\:{x}\: \\ $$$${find}\:{f}\left({x}\right)\: \\ $$
Commented by Tony Lin last updated on 22/Feb/20
![f(x+1)−f(x)=x ⇒f(0)=f(1) ⇒f(x)=kx(x−1)+c k[(x+1)x−x(x−1)]=x k=(1/2) ⇒f(x)=(1/2)x(x−1)+c](https://www.tinkutara.com/question/Q82578.png)
$${f}\left({x}+\mathrm{1}\right)−{f}\left({x}\right)={x} \\ $$$$\Rightarrow{f}\left(\mathrm{0}\right)={f}\left(\mathrm{1}\right) \\ $$$$\Rightarrow{f}\left({x}\right)={kx}\left({x}−\mathrm{1}\right)+{c} \\ $$$${k}\left[\left({x}+\mathrm{1}\right){x}−{x}\left({x}−\mathrm{1}\right)\right]={x} \\ $$$${k}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}{x}\left({x}−\mathrm{1}\right)+{c} \\ $$
