Question Number 17205 by Arnab Maiti last updated on 02/Jul/17
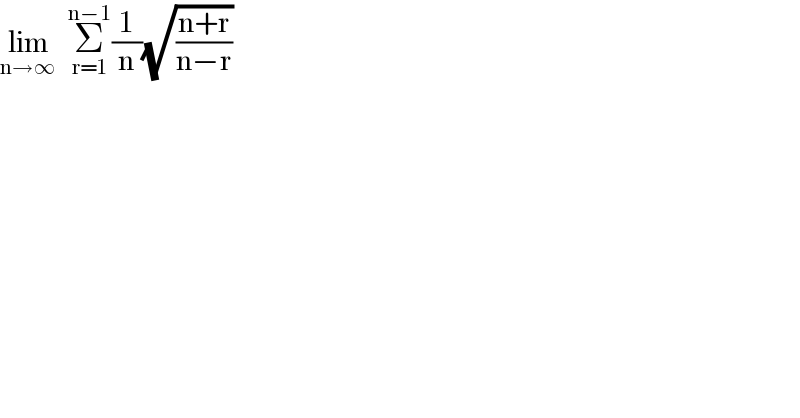
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\:\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\sqrt{\frac{\mathrm{n}+\mathrm{r}}{\mathrm{n}−\mathrm{r}}} \\ $$
Answered by ajfour last updated on 02/Jul/17
![(r/n)→x , ⇒ dx→(1/n) L=∫_0 ^( 1) (√((1+x)/(1−x))) dx let x=cos 2θ ⇒ dx=−2sin θcos θdθ for x=0 , θ=π/4 and when x=1, θ=0 since (√((1+cos 2θ)/(1−cos 2θ))) =∣((cos θ)/(sin θ))∣=((cos θ)/(sin θ)) in [0, π/4] so, L=∫_(π/4) ^( 0) ((cos θ)/(sin θ))(−2sin θcos θ)dθ L=∫_0 ^( π/4) (1+cos 2θ)dθ = (θ+((sin 2θ)/2))∣_0 ^(π/4) finally, L = (π/4)+(1/2) .](https://www.tinkutara.com/question/Q17207.png)
$$\frac{\mathrm{r}}{\mathrm{n}}\rightarrow\mathrm{x}\:,\:\Rightarrow\:\mathrm{dx}\rightarrow\frac{\mathrm{1}}{\mathrm{n}} \\ $$$$\mathrm{L}=\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \sqrt{\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}−\mathrm{x}}}\:\mathrm{dx} \\ $$$$\:\:\mathrm{let}\:\mathrm{x}=\mathrm{cos}\:\mathrm{2}\theta\:\:\Rightarrow\:\mathrm{dx}=−\mathrm{2sin}\:\theta\mathrm{cos}\:\theta\mathrm{d}\theta \\ $$$$\:\mathrm{for}\:\mathrm{x}=\mathrm{0}\:,\:\theta=\pi/\mathrm{4}\: \\ $$$$\:\:\mathrm{and}\:\mathrm{when}\:\mathrm{x}=\mathrm{1},\:\:\theta=\mathrm{0} \\ $$$$\mathrm{since}\:\:\:\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}}\:=\mid\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}\mid=\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}\: \\ $$$$\mathrm{in}\:\left[\mathrm{0},\:\pi/\mathrm{4}\right] \\ $$$$\mathrm{so},\:\:\mathrm{L}=\int_{\pi/\mathrm{4}} ^{\:\:\mathrm{0}} \:\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}\left(−\mathrm{2sin}\:\theta\mathrm{cos}\:\theta\right)\mathrm{d}\theta \\ $$$$\:\:\:\:\mathrm{L}=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \:\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)\mathrm{d}\theta \\ $$$$\:\:\:\:\:\:=\:\left(\theta+\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{\pi/\mathrm{4}} \\ $$$$\mathrm{finally},\:\:\:\:\:\mathrm{L}\:=\:\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
Commented by Arnab Maiti last updated on 02/Jul/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
