Question Number 132534 by liberty last updated on 15/Feb/21
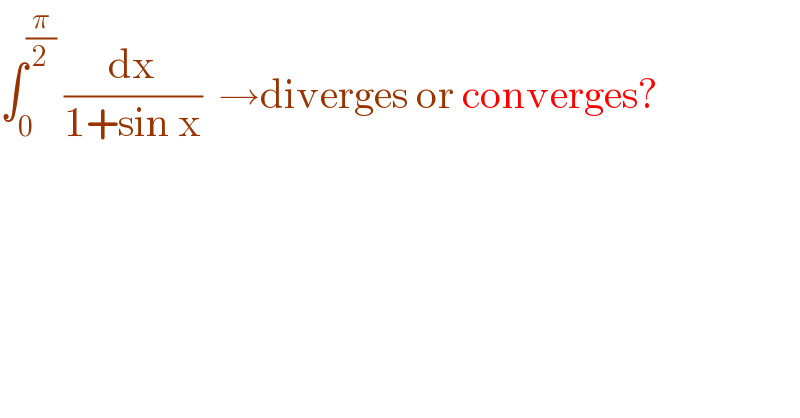
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}\:\:\rightarrow\mathrm{diverges}\:\mathrm{or}\:\mathrm{converges}? \\ $$
Commented by MJS_new last updated on 15/Feb/21
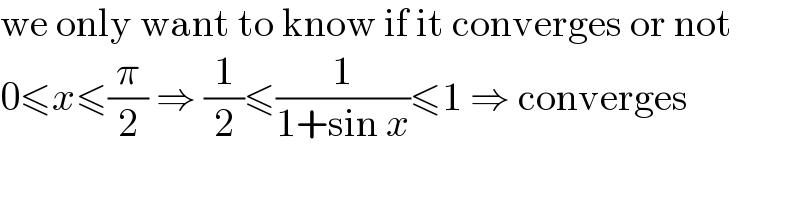
$$\mathrm{we}\:\mathrm{only}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{if}\:\mathrm{it}\:\mathrm{converges}\:\mathrm{or}\:\mathrm{not} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\leqslant\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:{x}}\leqslant\mathrm{1}\:\Rightarrow\:\mathrm{converges} \\ $$
Answered by Olaf last updated on 15/Feb/21
![Ω = ∫_0 ^(π/2) (dx/(1+sinx)) Ω = ∫_0 ^(π/2) (dx/(1+((2t)/(1+t^2 )))) with t = tan(x/2) Ω = ∫_0 ^(π/2) (1/(1+t^2 )).((2dt)/(1+t^2 )) Ω = −2[(1/(1+t))]_0 ^(π/2) = −2[(1/(1+tan(x/2)))]_0 ^(π/2) Ω = −2[(1/2)−1] = 1](https://www.tinkutara.com/question/Q132552.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+\mathrm{sin}{x}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\mathrm{with}\:{t}\:=\:\mathrm{tan}\frac{{x}}{\mathrm{2}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }.\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Omega\:=\:−\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{1}+{t}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\:−\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}\frac{{x}}{\mathrm{2}}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\Omega\:=\:−\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right]\:=\:\mathrm{1} \\ $$
Answered by EDWIN88 last updated on 15/Feb/21
![We want to evaluate ∫_( 0) ^( (π/2)) (dx/(1+sin x)) . I=∫_0 ^(π/2) (dx/(1+2sin ((x/2))cos ((x/2)))) Wierrstrass Substitution let tan ((x/2))= ∅ ⇒ { ((x=(π/2)→∅=1)),((x=0→∅=0)) :} dx = 2cos^2 ((x/2))d∅ I=∫_0 ^1 (1/(1+2((∅/(1+∅^2 ))))).((2/(1+∅^2 )))d∅ I= ∫_0 ^1 (2/((1+∅)^2 ))d∅ = −2 [(1/(1+∅)) ]_0 ^1 I=−2 [ (1/2)−1 ]= 1 (converges )](https://www.tinkutara.com/question/Q132536.png)
$$\:\mathrm{We}\:\mathrm{want}\:\mathrm{to}\:\mathrm{evaluate}\:\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}}\:. \\ $$$$\:\mathrm{I}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{2sin}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)} \\ $$$$\mathrm{Wierrstrass}\:\mathrm{Substitution} \\ $$$$\mathrm{let}\:\mathrm{tan}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\:\varnothing\:\Rightarrow\begin{cases}{\mathrm{x}=\frac{\pi}{\mathrm{2}}\rightarrow\varnothing=\mathrm{1}}\\{\mathrm{x}=\mathrm{0}\rightarrow\varnothing=\mathrm{0}}\end{cases} \\ $$$$\:\:\mathrm{dx}\:=\:\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{d}\varnothing \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}\left(\frac{\varnothing}{\mathrm{1}+\varnothing^{\mathrm{2}} }\right)}.\left(\frac{\mathrm{2}}{\mathrm{1}+\varnothing^{\mathrm{2}} }\right)\mathrm{d}\varnothing \\ $$$$\mathrm{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}}{\left(\mathrm{1}+\varnothing\right)^{\mathrm{2}} }\mathrm{d}\varnothing\:=\:−\mathrm{2}\:\left[\frac{\mathrm{1}}{\mathrm{1}+\varnothing}\:\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}=−\mathrm{2}\:\left[\:\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\:\right]=\:\mathrm{1}\:\left(\mathrm{converges}\:\right)\: \\ $$
Commented by liberty last updated on 15/Feb/21

Answered by Ar Brandon last updated on 15/Feb/21
![∫_0 ^(π/2) ((1−sinx)/(cos^2 x))dx=[tanx−(1/(cosx))]_0 ^(π/2) =1](https://www.tinkutara.com/question/Q132588.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}−\mathrm{sinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}=\left[\mathrm{tanx}−\frac{\mathrm{1}}{\mathrm{cosx}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{1} \\ $$
Commented by EDWIN88 last updated on 15/Feb/21
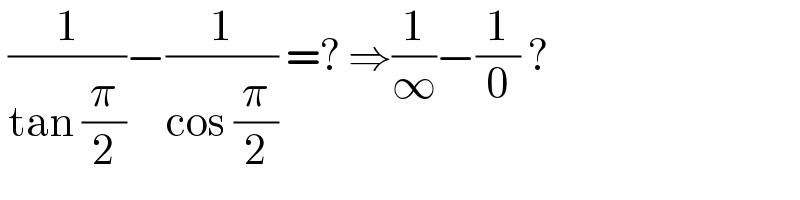
$$\:\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\pi}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{cos}\:\frac{\pi}{\mathrm{2}}}\:=?\:\Rightarrow\frac{\mathrm{1}}{\infty}−\frac{\mathrm{1}}{\mathrm{0}}\:?\: \\ $$
Commented by Ar Brandon last updated on 15/Feb/21
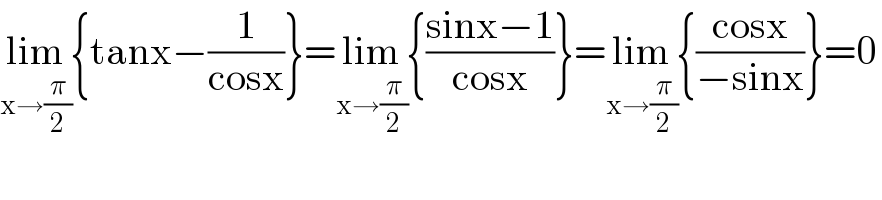
$$\underset{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left\{\mathrm{tanx}−\frac{\mathrm{1}}{\mathrm{cosx}}\right\}=\underset{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left\{\frac{\mathrm{sinx}−\mathrm{1}}{\mathrm{cosx}}\right\}=\underset{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left\{\frac{\mathrm{cosx}}{−\mathrm{sinx}}\right\}=\mathrm{0} \\ $$
Commented by Ar Brandon last updated on 15/Feb/21
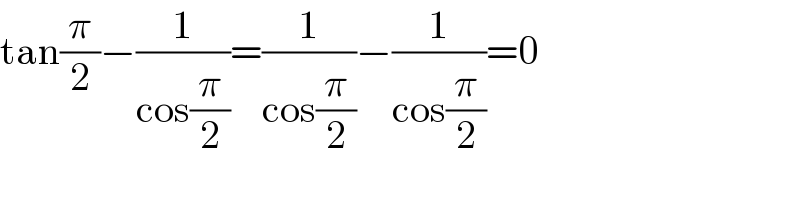
$$\mathrm{tan}\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{cos}\frac{\pi}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{cos}\frac{\pi}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{cos}\frac{\pi}{\mathrm{2}}}=\mathrm{0} \\ $$
