Question Number 82886 by 1406 last updated on 25/Feb/20
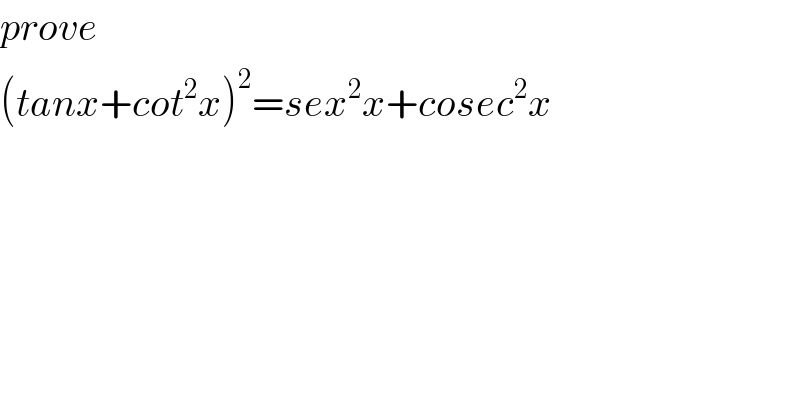
$${prove}\: \\ $$$$\left({tanx}+{cot}^{\mathrm{2}} {x}\right)^{\mathrm{2}} ={sex}^{\mathrm{2}} {x}+{cosec}^{\mathrm{2}} {x} \\ $$
Commented by jagoll last updated on 25/Feb/20
![⇒Rhs : sec^2 x+cosec^2 x = (1/(cos^2 x)) + (1/(sin^2 x)) = (4/((2sin xcos x)^2 )) = (4/(sin^2 2x)) ⇒Lhs : (((sin x)/(cos x)) + ((cos^2 x)/(sin^2 x)))^2 = (((sin^3 x+cos^3 x)/((1/2)sin xsin 2x)))^2 = 4((((sin^3 x+cos^3 x)^2 )/(sin^2 x sin^2 2x))) ((4[ (sin x+cos x)^2 (1−(1/2)sin 2x)^2 ])/(sin^2 x sin^2 2x)) = ((2 (1+sin 2x)(2−sin 2x))/(sin x sin^(2 ) 2x)) question wrong](https://www.tinkutara.com/question/Q82893.png)
$$\Rightarrow\mathrm{Rhs}\::\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}+\mathrm{cosec}\:^{\mathrm{2}} \mathrm{x}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:=\:\frac{\mathrm{4}}{\left(\mathrm{2sin}\:\mathrm{xcos}\:\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{4}}{\mathrm{sin}\:^{\mathrm{2}} \:\mathrm{2x}} \\ $$$$\Rightarrow\mathrm{Lhs}\::\:\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}\:+\:\frac{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\right)^{\mathrm{2}} =\: \\ $$$$\left(\frac{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{xsin}\:\mathrm{2x}}\right)^{\mathrm{2}} =\:\mathrm{4}\left(\frac{\left(\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}\right)^{\mathrm{2}} }{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{sin}\:^{\mathrm{2}} \:\mathrm{2x}}\right) \\ $$$$\frac{\mathrm{4}\left[\:\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2x}\right)^{\mathrm{2}} \right]}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{sin}\:^{\mathrm{2}} \:\mathrm{2x}} \\ $$$$=\:\frac{\mathrm{2}\:\left(\mathrm{1}+\mathrm{sin}\:\:\mathrm{2x}\right)\left(\mathrm{2}−\mathrm{sin}\:\mathrm{2x}\right)}{\mathrm{sin}\:\mathrm{x}\:\mathrm{sin}\:^{\mathrm{2}\:} \mathrm{2x}} \\ $$$$\mathrm{question}\:\mathrm{wrong} \\ $$
Commented by MJS last updated on 25/Feb/20
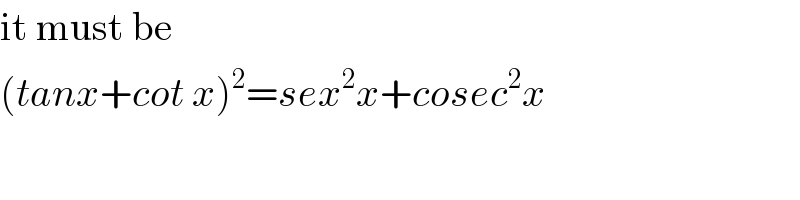
$$\mathrm{it}\:\mathrm{must}\:\mathrm{be} \\ $$$$\left({tanx}+{cot}\:{x}\right)^{\mathrm{2}} ={sex}^{\mathrm{2}} {x}+{cosec}^{\mathrm{2}} {x} \\ $$
