Question Number 83539 by jagoll last updated on 03/Mar/20
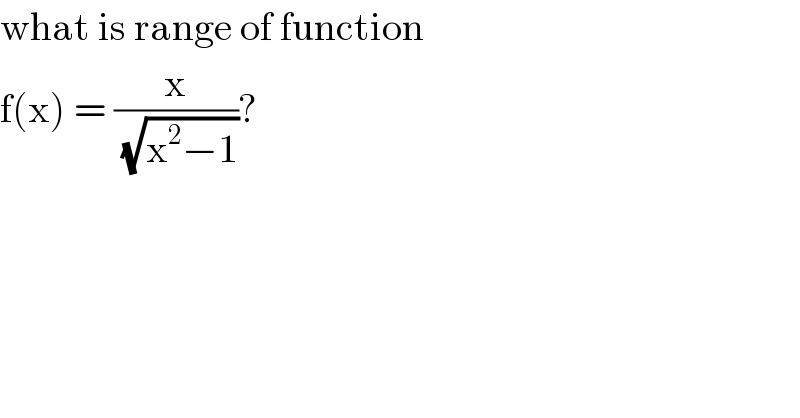
$$\mathrm{what}\:\mathrm{is}\:\mathrm{range}\:\mathrm{of}\:\mathrm{function}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}? \\ $$
Commented by john santu last updated on 03/Mar/20
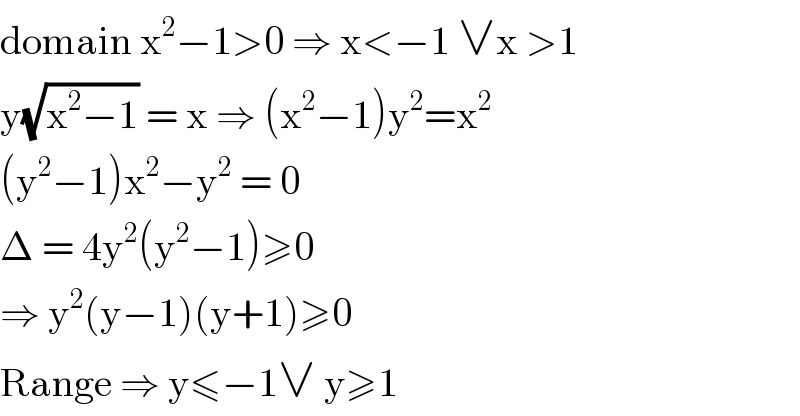
$$\mathrm{domain}\:\mathrm{x}^{\mathrm{2}} −\mathrm{1}>\mathrm{0}\:\Rightarrow\:\mathrm{x}<−\mathrm{1}\:\vee\mathrm{x}\:>\mathrm{1} \\ $$$$\mathrm{y}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:=\:\mathrm{x}\:\Rightarrow\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{y}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{y}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\Delta\:=\:\mathrm{4y}^{\mathrm{2}} \left(\mathrm{y}^{\mathrm{2}} −\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{y}^{\mathrm{2}} \left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{y}+\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{Range}\:\Rightarrow\:\mathrm{y}\leqslant−\mathrm{1}\vee\:\mathrm{y}\geqslant\mathrm{1}\: \\ $$
Commented by john santu last updated on 03/Mar/20
Commented by mathmax by abdo last updated on 03/Mar/20
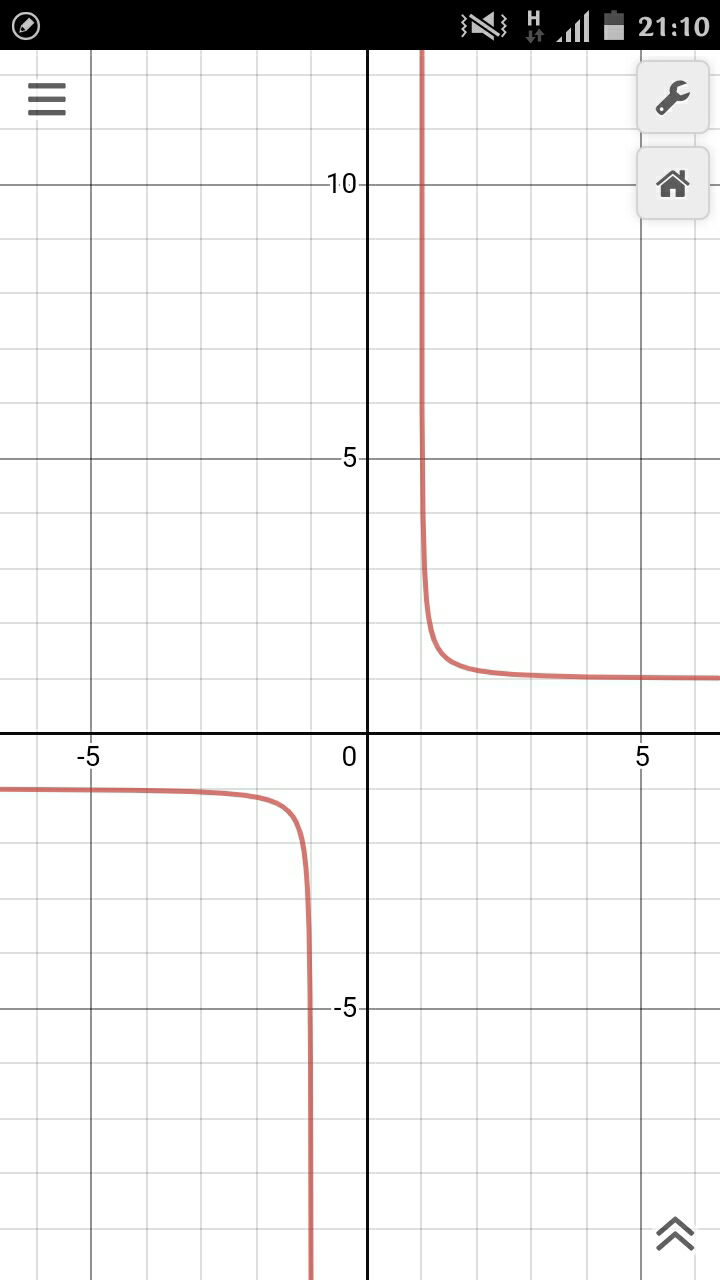
![f(x)=(x/( (√(x^2 −1)))) ⇒f defined on]−∞,−1[∪]1,+∞[ lim_(x→−∞) f(x) =lim_(x→−∞) (x/(∣x∣(√(1−x^(−2) )))) =−1 lim_(x→+∞) f(x)=lim_(x→+∞) (x/(x(√(1−x^(−2) )))) =1 f^′ (x)=(((√(x^2 −1))−x×((2x)/(2(√(x^2 −1)))))/(x^2 −1)) =((2(x^2 −1)−2x^2 )/(2(x^2 −1)(√(x^2 −1)))) =((−2)/(2(x^2 −1)(√(x^2 −1)))) =((−1)/((x^2 −1)(√(x^2 −1))))<0 ⇒f is decreasing on D_f x −∞ −1 1 +∞ f^′ − ∣∣ ∣∣ − f −1 decr−∞ +∞ decr 1 ⇒f(]−∞,−1[) =]−∞,−1[ and f(]1,+∞[)=[1,+∞[](https://www.tinkutara.com/question/Q83564.png)
$$\left.{f}\left({x}\right)=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow{f}\:{defined}\:{on}\right]−\infty,−\mathrm{1}\left[\cup\right]\mathrm{1},+\infty\left[\right. \\ $$$${lim}_{{x}\rightarrow−\infty} \:\:\:{f}\left({x}\right)\:={lim}_{{x}\rightarrow−\infty} \:\:\:\frac{{x}}{\mid{x}\mid\sqrt{\mathrm{1}−{x}^{−\mathrm{2}} }}\:=−\mathrm{1} \\ $$$${lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)={lim}_{{x}\rightarrow+\infty} \:\:\:\frac{{x}}{{x}\sqrt{\mathrm{1}−{x}^{−\mathrm{2}} }}\:=\mathrm{1} \\ $$$${f}^{'} \left({x}\right)=\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−{x}×\frac{\mathrm{2}{x}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}}{{x}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\frac{−\mathrm{2}}{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$=\frac{−\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}<\mathrm{0}\:\Rightarrow{f}\:{is}\:{decreasing}\:{on}\:{D}_{{f}} \\ $$$${x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$${f}^{'} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:− \\ $$$${f}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:{decr}−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty\:{decr}\:\mathrm{1} \\ $$$$\left.\Rightarrow{f}\left(\right]−\infty,−\mathrm{1}\left[\right)\:=\right]−\infty,−\mathrm{1}\left[\:\:{and}\:{f}\left(\right]\mathrm{1},+\infty\left[\right)=\left[\mathrm{1},+\infty\left[\right.\right.\right. \\ $$
