Question Number 149813 by mathdanisur last updated on 07/Aug/21
![∫(−1)^([x]) dx = ?](https://www.tinkutara.com/question/Q149813.png)
$$\int\left(−\mathrm{1}\right)^{\left[\boldsymbol{\mathrm{x}}\right]} \:\mathrm{dx}\:=\:? \\ $$
Commented by DonQuichote last updated on 07/Aug/21

$${deal}:\:{you}\:{show}\:{me}\:{your}\:{solution}\:{idea}\:{first} \\ $$$${then}\:{I}'{ll}\:{show}\:{you}\:{mine} \\ $$
Answered by mathmax by abdo last updated on 08/Aug/21
![f(x)=∫_0 ^x (−1)^([t]) dt ⇒f(x)=Σ_(k=0) ^([x]) ∫_k ^(k+1) (−1)^k dt +∫_([x]) ^x (−1)^([t]) dt =Σ_(k=0) ^([x]) (−1)^k +∫_([x]) ^x (−1)^([t]) dt =((1−(−1)^([x]+1) )/2) +∫_([x]) ^x (−1)^([t]) dt if x from N ∫_([x]) ^x (−1)^([t]) dt=0 ⇒∫_0 ^x (−1)^([t]) dt=((1−(−1)^(x+1) )/2)](https://www.tinkutara.com/question/Q149882.png)
$$\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{x}} \:\left(−\mathrm{1}\right)^{\left[\mathrm{t}\right]} \:\mathrm{dt}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\left[\mathrm{x}\right]} \:\int_{\mathrm{k}} ^{\mathrm{k}+\mathrm{1}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{dt}\:+\int_{\left[\mathrm{x}\right]} ^{\mathrm{x}} \:\left(−\mathrm{1}\right)^{\left[\mathrm{t}\right]} \:\mathrm{dt} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\left[\mathrm{x}\right]} \:\left(−\mathrm{1}\right)^{\mathrm{k}} +\int_{\left[\mathrm{x}\right]} ^{\mathrm{x}} \left(−\mathrm{1}\right)^{\left[\mathrm{t}\right]} \mathrm{dt}\:=\frac{\mathrm{1}−\left(−\mathrm{1}\right)^{\left[\mathrm{x}\right]+\mathrm{1}} }{\mathrm{2}}\:+\int_{\left[\mathrm{x}\right]} ^{\mathrm{x}} \:\left(−\mathrm{1}\right)^{\left[\mathrm{t}\right]} \:\mathrm{dt} \\ $$$$\mathrm{if}\:\mathrm{x}\:\mathrm{from}\:\mathrm{N}\:\:\int_{\left[\mathrm{x}\right]} ^{\mathrm{x}} \:\left(−\mathrm{1}\right)^{\left[\mathrm{t}\right]} \:\mathrm{dt}=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{x}} \:\left(−\mathrm{1}\right)^{\left[\mathrm{t}\right]} \:\mathrm{dt}=\frac{\mathrm{1}−\left(−\mathrm{1}\right)^{\mathrm{x}+\mathrm{1}} }{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 08/Aug/21
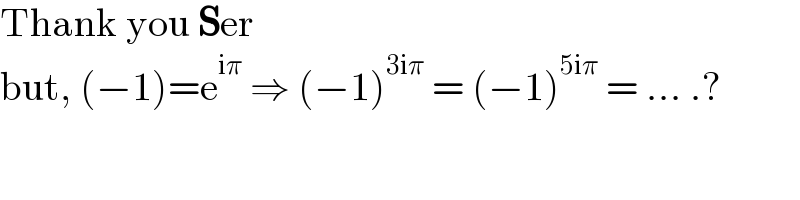
$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$$$\mathrm{but},\:\left(−\mathrm{1}\right)=\mathrm{e}^{\mathrm{i}\pi} \:\Rightarrow\:\left(−\mathrm{1}\right)^{\mathrm{3i}\pi} \:=\:\left(−\mathrm{1}\right)^{\mathrm{5i}\pi} \:=\:…\:.? \\ $$
