Question Number 19268 by khamizan833@yahoo.com last updated on 08/Aug/17
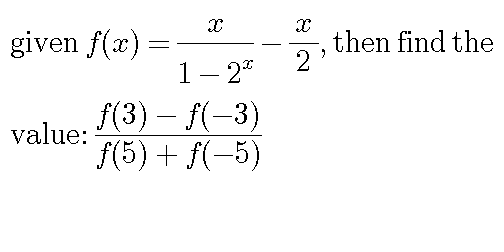
Answered by ajfour last updated on 08/Aug/17
![f(x)=x((1/(1−2^x ))−(1/2)) f(x)+f(−x)=x[((1/(1−2^x ))−(1/2))−((2^x /(2^x −1))−(1/2))] =−(((2^x +1)x)/((2^x −1))) ⇒ f(5)+f(−5)=−((33×5)/(31))=−((165)/(31)) f(x)−f(−x)=x[((1/(1−2^x ))−(1/2))+((2^x /(2^x −1))−(1/2))] =0 ⇒ f(3)−f(−3)=0 so, ((f(3)−f(−3))/(f(5)+f(−5))) =0 .](https://www.tinkutara.com/question/Q19269.png)
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2}^{\mathrm{x}} }−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(−\mathrm{x}\right)=\mathrm{x}\left[\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2}^{\mathrm{x}} }−\frac{\mathrm{1}}{\mathrm{2}}\right)−\left(\frac{\mathrm{2}^{\mathrm{x}} }{\mathrm{2}^{\mathrm{x}} −\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=−\frac{\left(\mathrm{2}^{\mathrm{x}} +\mathrm{1}\right)\mathrm{x}}{\left(\mathrm{2}^{\mathrm{x}} −\mathrm{1}\right)} \\ $$$$\Rightarrow\:\mathrm{f}\left(\mathrm{5}\right)+\mathrm{f}\left(−\mathrm{5}\right)=−\frac{\mathrm{33}×\mathrm{5}}{\mathrm{31}}=−\frac{\mathrm{165}}{\mathrm{31}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)−\mathrm{f}\left(−\mathrm{x}\right)=\mathrm{x}\left[\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2}^{\mathrm{x}} }−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{2}^{\mathrm{x}} }{\mathrm{2}^{\mathrm{x}} −\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{f}\left(\mathrm{3}\right)−\mathrm{f}\left(−\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{so},\:\:\:\frac{\mathrm{f}\left(\mathrm{3}\right)−\mathrm{f}\left(−\mathrm{3}\right)}{\mathrm{f}\left(\mathrm{5}\right)+\mathrm{f}\left(−\mathrm{5}\right)}\:=\mathrm{0}\:. \\ $$
Commented by khamizan833@yahoo.com last updated on 08/Aug/17
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much},\mathrm{sir}. \\ $$
