Menu Close

solve-I-0-1-Arcsin-x-1-x-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 150356 by mnjuly1970 last updated on 11/Aug/21
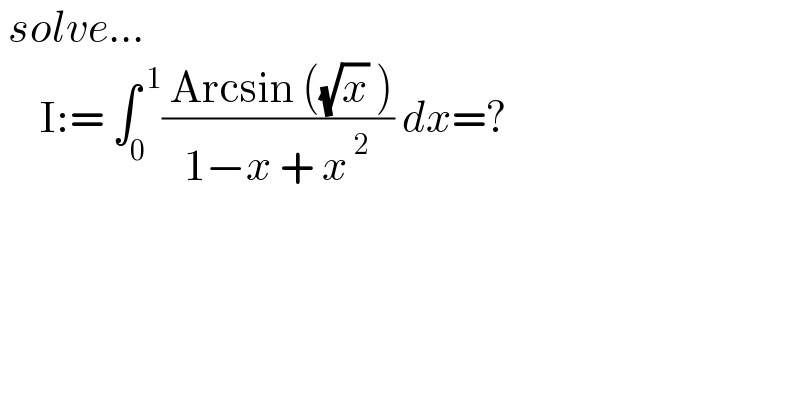
solve... I:= ∫_0 ^( 1) (( Arcsin ((√x) ))/(1−x + x^( 2) )) dx=?
$$\:{solve}… \\ $$$$\:\:\:\:\:\mathrm{I}:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\mathrm{Arcsin}\:\left(\sqrt{{x}}\:\right)}{\mathrm{1}−{x}\:+\:{x}^{\:\mathrm{2}} }\:{dx}=? \\ $$
Answered by Lordose last updated on 12/Aug/21
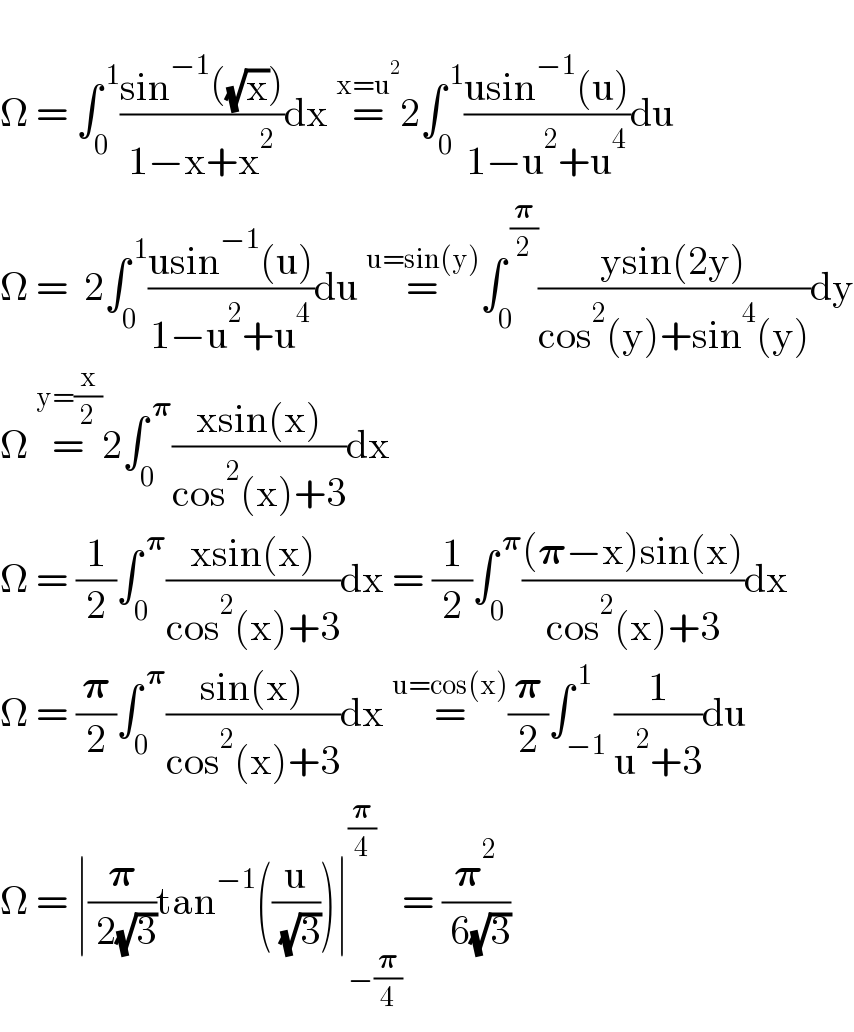
Ω = ∫_0 ^( 1) ((sin^(−1) ((√x)))/(1−x+x^2 ))dx =^(x=u^2 ) 2∫_0 ^( 1) ((usin^(−1) (u))/(1−u^2 +u^4 ))du Ω = 2∫_0 ^( 1) ((usin^(−1) (u))/(1−u^2 +u^4 ))du =^(u=sin(y)) ∫_0 ^( (𝛑/2)) ((ysin(2y))/(cos^2 (y)+sin^4 (y)))dy Ω =^(y=(x/2)) 2∫_0 ^( 𝛑) ((xsin(x))/(cos^2 (x)+3))dx Ω = (1/2)∫_0 ^( 𝛑) ((xsin(x))/(cos^2 (x)+3))dx = (1/2)∫_0 ^( 𝛑) (((𝛑−x)sin(x))/(cos^2 (x)+3))dx Ω = (𝛑/2)∫_0 ^( 𝛑) ((sin(x))/(cos^2 (x)+3))dx =^(u=cos(x)) (𝛑/2)∫_(−1) ^( 1) (1/(u^2 +3))du Ω = ∣(𝛑/( 2(√3)))tan^(−1) ((u/( (√3))))∣_(−(𝛑/4)) ^(𝛑/4) = (𝛑^2 /( 6(√3)))
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)}{\mathrm{1}−\mathrm{x}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\overset{\mathrm{x}=\mathrm{u}^{\mathrm{2}} } {=}\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{usin}^{−\mathrm{1}} \left(\mathrm{u}\right)}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} +\mathrm{u}^{\mathrm{4}} }\mathrm{du} \\ $$$$\Omega\:=\:\:\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{usin}^{−\mathrm{1}} \left(\mathrm{u}\right)}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} +\mathrm{u}^{\mathrm{4}} }\mathrm{du}\:\overset{\mathrm{u}=\mathrm{sin}\left(\mathrm{y}\right)} {=}\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\mathrm{ysin}\left(\mathrm{2y}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{y}\right)+\mathrm{sin}^{\mathrm{4}} \left(\mathrm{y}\right)}\mathrm{dy} \\ $$$$\Omega\:\overset{\mathrm{y}=\frac{\mathrm{x}}{\mathrm{2}}} {=}\mathrm{2}\int_{\mathrm{0}} ^{\:\boldsymbol{\pi}} \frac{\mathrm{xsin}\left(\mathrm{x}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{3}}\mathrm{dx}\: \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\boldsymbol{\pi}} \frac{\mathrm{xsin}\left(\mathrm{x}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{3}}\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\boldsymbol{\pi}} \frac{\left(\boldsymbol{\pi}−\mathrm{x}\right)\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{3}}\mathrm{dx} \\ $$$$\Omega\:=\:\frac{\boldsymbol{\pi}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\boldsymbol{\pi}} \frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{3}}\mathrm{dx}\:\overset{\mathrm{u}=\mathrm{cos}\left(\mathrm{x}\right)} {=}\frac{\boldsymbol{\pi}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} +\mathrm{3}}\mathrm{du} \\ $$$$\Omega\:=\:\mid\frac{\boldsymbol{\pi}}{\:\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{u}}{\:\sqrt{\mathrm{3}}}\right)\mid_{−\frac{\boldsymbol{\pi}}{\mathrm{4}}} ^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} =\:\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\:\mathrm{6}\sqrt{\mathrm{3}}} \\ $$
Answered by mindispower last updated on 11/Aug/21
f(x)=1−x+x^2 f(1−x)=1−(1−x)+(1−x)^2 =1−x+x^2 x→1−x I=∫_0 ^1 ((arcsin(√((1−x))))/(1−x+x^2 ))dx arcsin(a)+arcsin(b)=arcsin(a(√(1−b^2 ))+b(√(1−a^2 ))) arcsin((√(1−x)))+arcsin((√x))=arcsin((1−x)(√(1−(√x^2 )+(√x).(√(1−((√(1−x)^2 ))))))) x∈[0,1[ (√((1−x)^2 ))=1−x =arcsin(1−x+x)=arcsin(1)=(π/2) 2I=∫_0 ^1 ((arcsin((√(1−x))))/(1−x+x^2 ))dx+∫_0 ^1 ((arcsin((√x)))/(1−x+x^2 ))dx 2I=∫_0 ^1 ((arcsin((√x))+arcsim((√(1−x))))/(1−x+x^2 ))dx =(π/2)∫_0 ^1 (dx/(1−x+x^2 ))=(π/2)∫_0 ^1 (dx/((x−(1/2))^2 +(3/4))) =(π/2)[(2/( (√3)))arctan((2/( (√3)))(x−(1/2))]_0 ^1 =(π/( (√3))).(π/3)=((2π^2 )/(3(√3))) I=(π^2 /(3(√3)))
$${f}\left({x}\right)=\mathrm{1}−{x}+{x}^{\mathrm{2}} \\ $$$${f}\left(\mathrm{1}−{x}\right)=\mathrm{1}−\left(\mathrm{1}−{x}\right)+\left(\mathrm{1}−{x}\right)^{\mathrm{2}} =\mathrm{1}−{x}+{x}^{\mathrm{2}} \\ $$$${x}\rightarrow\mathrm{1}−{x} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arcsin}\sqrt{\left(\mathrm{1}−{x}\right)}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$$${arcsin}\left({a}\right)+{arcsin}\left({b}\right)={arcsin}\left({a}\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }+{b}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }\right) \\ $$$${arcsin}\left(\sqrt{\mathrm{1}−{x}}\right)+{arcsin}\left(\sqrt{{x}}\right)={arcsin}\left(\left(\mathrm{1}−{x}\right)\sqrt{\left.\mathrm{1}−\sqrt{{x}^{\mathrm{2}} }+\sqrt{{x}}.\sqrt{\mathrm{1}−\left(\sqrt{\left.\mathrm{1}−{x}\right)^{\mathrm{2}} }\right.}\right)}\right. \\ $$$${x}\in\left[\mathrm{0},\mathrm{1}\left[\:\sqrt{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\mathrm{1}−{x}\right.\right. \\ $$$$={arcsin}\left(\mathrm{1}−{x}+{x}\right)={arcsin}\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arcsin}\left(\sqrt{\mathrm{1}−{x}}\right)}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arcsin}\left(\sqrt{{x}}\right)}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arcsin}\left(\sqrt{{x}}\right)+{arcsim}\left(\sqrt{\left.\mathrm{1}−{x}\right)}\right.}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\frac{\pi}{\mathrm{2}}\left[\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \right. \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{3}}}.\frac{\pi}{\mathrm{3}}=\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$${I}=\frac{\pi^{\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Answered by Kamel last updated on 11/Aug/21
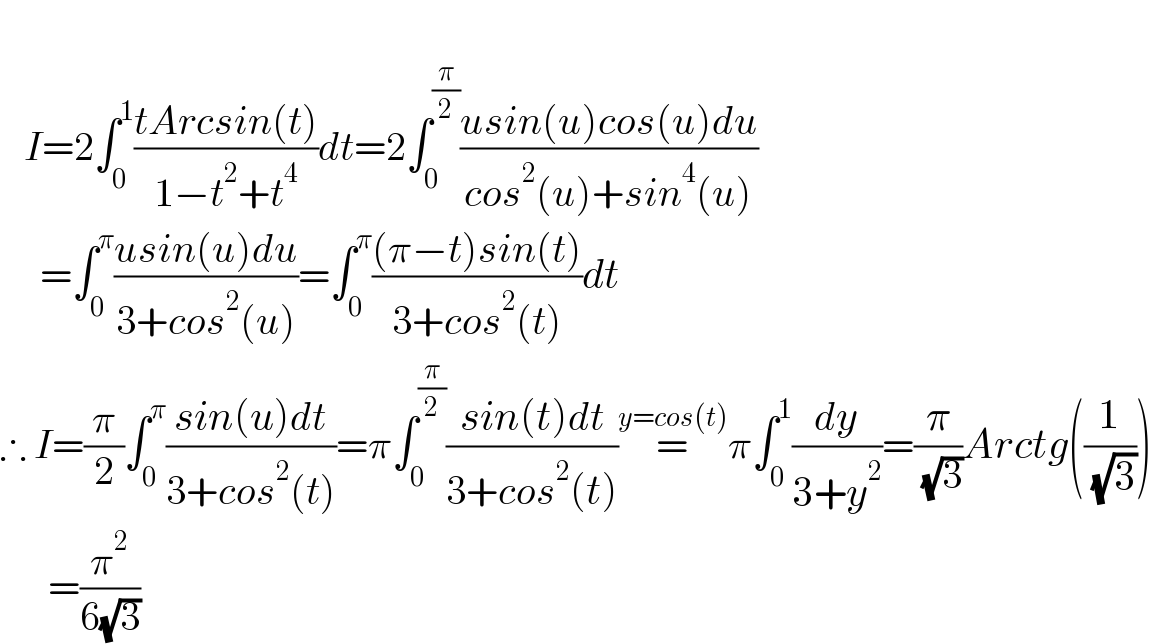
I=2∫_0 ^1 ((tArcsin(t))/(1−t^2 +t^4 ))dt=2∫_0 ^(π/2) ((usin(u)cos(u)du)/(cos^2 (u)+sin^4 (u))) =∫_0 ^π ((usin(u)du)/(3+cos^2 (u)))=∫_0 ^π (((π−t)sin(t))/(3+cos^2 (t)))dt ∴ I=(π/2)∫_0 ^π ((sin(u)dt)/(3+cos^2 (t)))=π∫_0 ^(π/2) ((sin(t)dt)/(3+cos^2 (t)))=^(y=cos(t)) π∫_0 ^1 (dy/(3+y^2 ))=(π/( (√3)))Arctg((1/( (√3)))) =(π^2 /(6(√3)))
$$ \\ $$$$\:\:\:{I}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{tArcsin}\left({t}\right)}{\mathrm{1}−{t}^{\mathrm{2}} +{t}^{\mathrm{4}} }{dt}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{usin}\left({u}\right){cos}\left({u}\right){du}}{{cos}^{\mathrm{2}} \left({u}\right)+{sin}^{\mathrm{4}} \left({u}\right)} \\ $$$$\:\:\:\:\:=\int_{\mathrm{0}} ^{\pi} \frac{{usin}\left({u}\right){du}}{\mathrm{3}+{cos}^{\mathrm{2}} \left({u}\right)}=\int_{\mathrm{0}} ^{\pi} \frac{\left(\pi−{t}\right){sin}\left({t}\right)}{\mathrm{3}+{cos}^{\mathrm{2}} \left({t}\right)}{dt} \\ $$$$\therefore\:{I}=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \frac{{sin}\left({u}\right){dt}}{\mathrm{3}+{cos}^{\mathrm{2}} \left({t}\right)}=\pi\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}\left({t}\right){dt}}{\mathrm{3}+{cos}^{\mathrm{2}} \left({t}\right)}\overset{{y}={cos}\left({t}\right)} {=}\pi\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dy}}{\mathrm{3}+{y}^{\mathrm{2}} }=\frac{\pi}{\:\sqrt{\mathrm{3}}}{Arctg}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$\:\:\:\:\:\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}\sqrt{\mathrm{3}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *