Question Number 85236 by jagoll last updated on 20/Mar/20
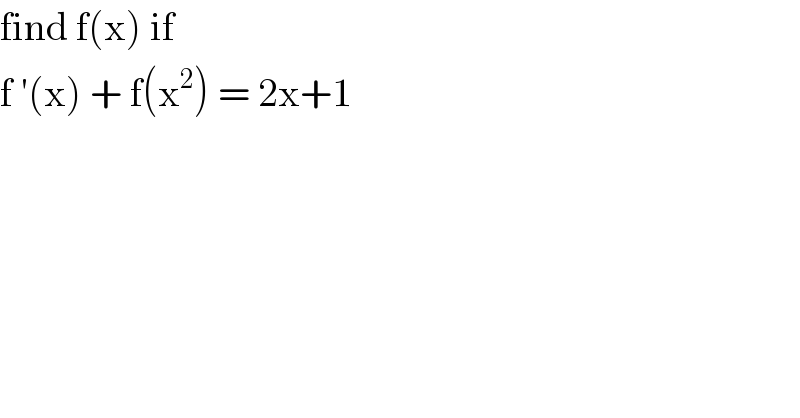
$$\mathrm{find}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{if}\: \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)\:+\:\mathrm{f}\left(\mathrm{x}^{\mathrm{2}} \right)\:=\:\mathrm{2x}+\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 20/Mar/20
![its clear that f is polynomial let f(x)=Σ_(n=0) ^∞ a_n x^n f^′ (x) =Σ_(n=1) ^∞ na_n x^(n−1) =Σ_(n=0) ^∞ (n+1)a_(n+1) x^n f(x^2 ) =Σ_(n=0) ^∞ a_n x^(2n) ⇒ Σ_(n=0) ^∞ (n+1)a_(n+1) x^n +Σ_(n=0) ^∞ a_n x^(2n) =2x+1 changement of indice 2n =p ⇒Σ_(n=0) ^∞ (n+1)a_n x^n +Σ_(p=0) ^∞ a_([(p/2)]) x^p =2x+1 ⇒ Σ_(n=0) ^∞ {(n+1)a_n +a_([(n/2)]) }x^n =2x+1 ⇒ { ((a_0 +a_0 =1)),((2a_1 +a_0 =2 and (n+1)a_n +a_([(n/2)]) =0 ∀n≥2 ⇒)) :} { ((a_0 =(1/2) and a_n =−(a_([(n/2)]) /(n+1)) ∀n≥2)),((a_1 =(3/4))) :} a_2 =−(a_1 /3) , a_3 =−(a_1 /4) .....](https://www.tinkutara.com/question/Q85310.png)
$${its}\:{clear}\:{that}\:{f}\:{is}\:{polynomial}\:{let}\:{f}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:{a}_{{n}} {x}^{{n}} \\ $$$${f}^{'} \left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{na}_{{n}} {x}^{{n}−\mathrm{1}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left({n}+\mathrm{1}\right){a}_{{n}+\mathrm{1}} {x}^{{n}} \\ $$$${f}\left({x}^{\mathrm{2}} \right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{a}_{{n}} {x}^{\mathrm{2}{n}} \:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\left({n}+\mathrm{1}\right){a}_{{n}+\mathrm{1}} {x}^{{n}} \:+\sum_{{n}=\mathrm{0}} ^{\infty} \:{a}_{{n}} {x}^{\mathrm{2}{n}} \:\:=\mathrm{2}{x}+\mathrm{1}\:\:{changement}\:{of}\: \\ $$$${indice}\:\:\mathrm{2}{n}\:={p}\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \left({n}+\mathrm{1}\right){a}_{{n}} {x}^{{n}} \:+\sum_{{p}=\mathrm{0}} ^{\infty} \:{a}_{\left[\frac{{p}}{\mathrm{2}}\right]} \:\:{x}^{{p}} \:=\mathrm{2}{x}+\mathrm{1}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \left\{\left({n}+\mathrm{1}\right){a}_{{n}} \:+{a}_{\left[\frac{{n}}{\mathrm{2}}\right]} \right\}{x}^{{n}} \:=\mathrm{2}{x}+\mathrm{1}\:\Rightarrow \\ $$$$\begin{cases}{{a}_{\mathrm{0}} +{a}_{\mathrm{0}} =\mathrm{1}}\\{\mathrm{2}{a}_{\mathrm{1}} +{a}_{\mathrm{0}} =\mathrm{2}\:\:\:{and}\:\:\left({n}+\mathrm{1}\right){a}_{{n}} \:+{a}_{\left[\frac{{n}}{\mathrm{2}}\right]} \:=\mathrm{0}\:\:\forall{n}\geqslant\mathrm{2}\:\Rightarrow}\end{cases} \\ $$$$\begin{cases}{{a}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:{and}\:\:{a}_{{n}} =−\frac{{a}_{\left[\frac{{n}}{\mathrm{2}}\right]} }{{n}+\mathrm{1}}\:\:\:\forall{n}\geqslant\mathrm{2}}\\{{a}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{4}}}\end{cases} \\ $$$${a}_{\mathrm{2}} =−\frac{{a}_{\mathrm{1}} }{\mathrm{3}}\:\:\:\:,\:\:{a}_{\mathrm{3}} =−\frac{{a}_{\mathrm{1}} }{\mathrm{4}}\:….. \\ $$
Answered by john santu last updated on 20/Mar/20

$$\frac{\mathrm{df}}{\mathrm{dx}}\:=\:\mathrm{2x}+\mathrm{1}\:−\:\mathrm{f}\left(\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\mathrm{df}\:=\:\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{dx}−\mathrm{f}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\int\:\mathrm{df}\:=\:\int\:\left(\mathrm{2x}+\mathrm{1}\right)\:\mathrm{dx}\:−\:\int\:\mathrm{f}\left(\mathrm{x}^{\mathrm{2}} \right)\:\mathrm{dx} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}\:−\:\int\:\mathrm{f}\left(\mathrm{x}^{\mathrm{2}} \right)\:\mathrm{dx}\: \\ $$$$\mathrm{K}\:=\:\int\:\mathrm{f}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{u}=\mathrm{x}^{\mathrm{2}} \:\Rightarrow\mathrm{du}\:=\:\mathrm{2x}\:\mathrm{dx} \\ $$$$\mathrm{dx}\:=\:\frac{\mathrm{du}}{\mathrm{2}\sqrt{\mathrm{u}}} \\ $$$$\mathrm{K}\:=\:\int\:\mathrm{f}\left(\mathrm{u}\right)\:×\:\frac{\mathrm{2du}}{\:\sqrt{\mathrm{u}}\:}\: \\ $$$$ \\ $$
Commented by jagoll last updated on 20/Mar/20

$$\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\int\:{f}\left({u}\right)×\:\frac{\mathrm{2}{du}}{\:\sqrt{{u}}} \\ $$
