Question Number 20053 by Tinkutara last updated on 21/Aug/17
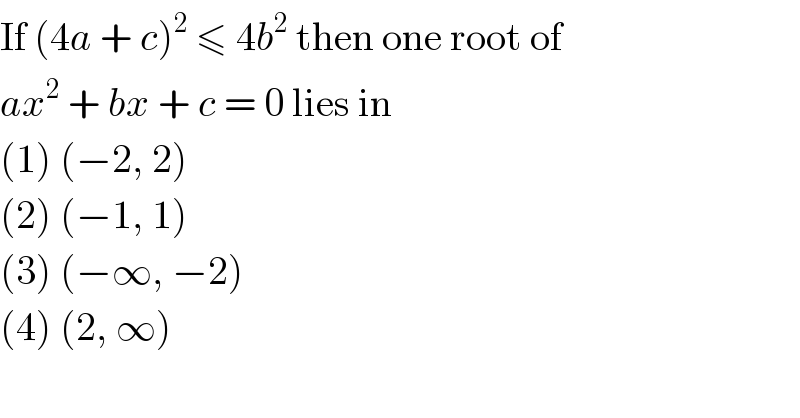
$$\mathrm{If}\:\left(\mathrm{4}{a}\:+\:{c}\right)^{\mathrm{2}} \:\leqslant\:\mathrm{4}{b}^{\mathrm{2}} \:\mathrm{then}\:\mathrm{one}\:\mathrm{root}\:\mathrm{of} \\ $$$${ax}^{\mathrm{2}} \:+\:{bx}\:+\:{c}\:=\:\mathrm{0}\:\mathrm{lies}\:\mathrm{in} \\ $$$$\left(\mathrm{1}\right)\:\left(−\mathrm{2},\:\mathrm{2}\right) \\ $$$$\left(\mathrm{2}\right)\:\left(−\mathrm{1},\:\mathrm{1}\right) \\ $$$$\left(\mathrm{3}\right)\:\left(−\infty,\:−\mathrm{2}\right) \\ $$$$\left(\mathrm{4}\right)\:\left(\mathrm{2},\:\infty\right) \\ $$
Answered by ajfour last updated on 21/Aug/17
![(4a+c)^2 −4b^2 ≤ 0 ⇒ (4a+2b+c)(4a−2b+c) ≤0 ⇒ f(2)f(−2)≤0 ⇒ f(x) changes sign or is zero in [−2,2], hence one root lies in [−2, 2].](https://www.tinkutara.com/question/Q20067.png)
$$\left(\mathrm{4}{a}+{c}\right)^{\mathrm{2}} −\mathrm{4}{b}^{\mathrm{2}} \:\leqslant\:\mathrm{0} \\ $$$$\Rightarrow\:\:\left(\mathrm{4}{a}+\mathrm{2}{b}+{c}\right)\left(\mathrm{4}{a}−\mathrm{2}{b}+{c}\right)\:\leqslant\mathrm{0} \\ $$$$\Rightarrow\:\:{f}\left(\mathrm{2}\right){f}\left(−\mathrm{2}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\:\:{f}\left({x}\right)\:{changes}\:{sign}\:{or}\:{is}\:{zero}\: \\ $$$${in}\:\left[−\mathrm{2},\mathrm{2}\right],\:{hence}\:{one}\:{root} \\ $$$${lies}\:{in}\:\left[−\mathrm{2},\:\mathrm{2}\right]. \\ $$
Commented by Tinkutara last updated on 21/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
