Question Number 85653 by M±th+et£s last updated on 23/Mar/20
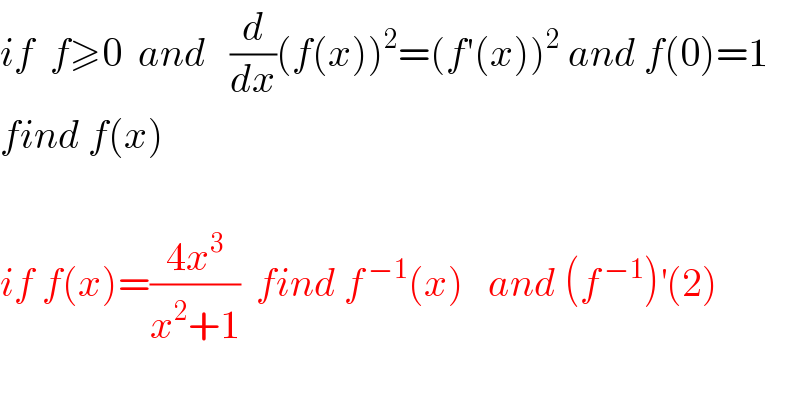
$${if}\:\:{f}\geqslant\mathrm{0}\:\:{and}\:\:\:\frac{{d}}{{dx}}\left({f}\left({x}\right)\right)^{\mathrm{2}} =\left({f}'\left({x}\right)\right)^{\mathrm{2}} \:{and}\:{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${find}\:{f}\left({x}\right)\:\:\: \\ $$$$ \\ $$$${if}\:{f}\left({x}\right)=\frac{\mathrm{4}{x}^{\mathrm{3}} }{{x}^{\mathrm{2}} +\mathrm{1}}\:\:{find}\:{f}^{\:−\mathrm{1}} \left({x}\right)\:\:\:{and}\:\left({f}^{\:−\mathrm{1}} \right)^{'} \left(\mathrm{2}\right) \\ $$
Commented by john santu last updated on 24/Mar/20
![(1) 2f(x) f ′(x) = (f ′(x))^2 f ′(x)[ f ′(x)−2f(x)] = 0 ⇒f ′(x) = 0 ⇒ f(x) = k , k=constan f(0) = 1 ⇒ k = 1 ⇒f(x)=1 ⇒f ′(x) = 2f(x) df(x) = 2f(x) dx ∫ df(x) = ∫ 2f(x) dx f(x)= 2∫f(x)dx](https://www.tinkutara.com/question/Q85679.png)
$$\left(\mathrm{1}\right)\:\mathrm{2}{f}\left({x}\right)\:{f}\:'\left({x}\right)\:=\:\left({f}\:'\left({x}\right)\right)^{\mathrm{2}} \\ $$$${f}\:'\left({x}\right)\left[\:{f}\:'\left({x}\right)−\mathrm{2}{f}\left({x}\right)\right]\:=\:\mathrm{0} \\ $$$$\Rightarrow{f}\:'\left({x}\right)\:=\:\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)\:=\:{k}\:,\:{k}={constan} \\ $$$${f}\left(\mathrm{0}\right)\:=\:\mathrm{1}\:\Rightarrow\:{k}\:=\:\mathrm{1}\:\Rightarrow{f}\left({x}\right)=\mathrm{1} \\ $$$$\Rightarrow{f}\:'\left({x}\right)\:=\:\mathrm{2}{f}\left({x}\right)\: \\ $$$${df}\left({x}\right)\:=\:\mathrm{2}{f}\left({x}\right)\:{dx} \\ $$$$\int\:{df}\left({x}\right)\:=\:\int\:\mathrm{2}{f}\left({x}\right)\:{dx} \\ $$$${f}\left({x}\right)=\:\mathrm{2}\int{f}\left({x}\right){dx} \\ $$
