Question-21021

Question Number 21021 by youssoufab last updated on 10/Sep/17

Commented by $@ty@m last updated on 10/Sep/17

$${pl}.\:{translate}\:{into}\:{English} \\ $$

Commented by Joel577 last updated on 10/Sep/17

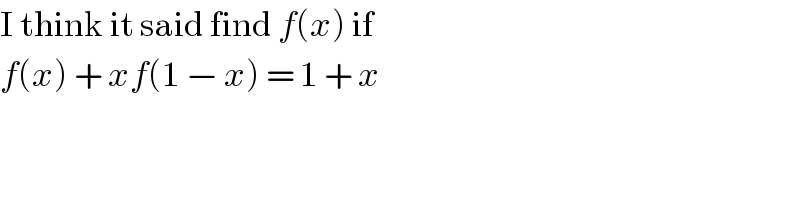
I think it said find f(x) if f(x) + xf(1 − x) = 1 + x

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{said}\:\mathrm{find}\:{f}\left({x}\right)\:\mathrm{if}\: \\ $$$${f}\left({x}\right)\:+\:{xf}\left(\mathrm{1}\:−\:{x}\right)\:=\:\mathrm{1}\:+\:{x} \\ $$

Answered by $@ty@m last updated on 11/Sep/17

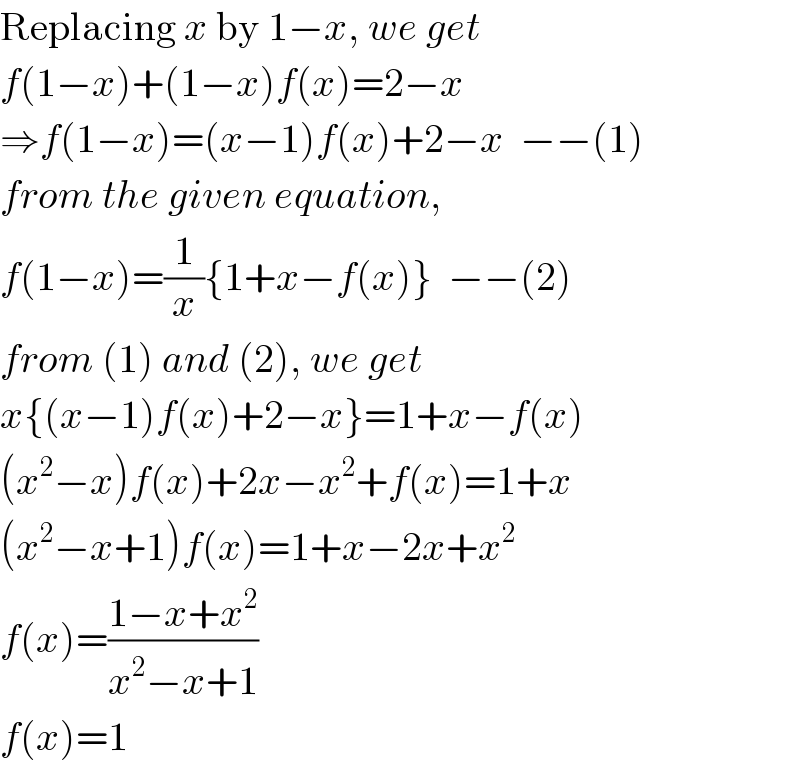
Replacing x by 1−x, we get f(1−x)+(1−x)f(x)=2−x ⇒f(1−x)=(x−1)f(x)+2−x −−(1) from the given equation, f(1−x)=(1/x){1+x−f(x)} −−(2) from (1) and (2), we get x{(x−1)f(x)+2−x}=1+x−f(x) (x^2 −x)f(x)+2x−x^2 +f(x)=1+x (x^2 −x+1)f(x)=1+x−2x+x^2 f(x)=((1−x+x^2 )/(x^2 −x+1)) f(x)=1

$$\mathrm{Replacing}\:{x}\:\mathrm{by}\:\mathrm{1}−{x},\:{we}\:{get} \\ $$$${f}\left(\mathrm{1}−{x}\right)+\left(\mathrm{1}−{x}\right){f}\left({x}\right)=\mathrm{2}−{x} \\ $$$$\Rightarrow{f}\left(\mathrm{1}−{x}\right)=\left({x}−\mathrm{1}\right){f}\left({x}\right)+\mathrm{2}−{x}\:\:−−\left(\mathrm{1}\right) \\ $$$${from}\:{the}\:{given}\:{equation}, \\ $$$${f}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{1}}{{x}}\left\{\mathrm{1}+{x}−{f}\left({x}\right)\right\}\:\:−−\left(\mathrm{2}\right) \\ $$$${from}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right),\:{we}\:{get} \\ $$$${x}\left\{\left({x}−\mathrm{1}\right){f}\left({x}\right)+\mathrm{2}−{x}\right\}=\mathrm{1}+{x}−{f}\left({x}\right) \\ $$$$\left({x}^{\mathrm{2}} −{x}\right){f}\left({x}\right)+\mathrm{2}{x}−{x}^{\mathrm{2}} +{f}\left({x}\right)=\mathrm{1}+{x} \\ $$$$\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right){f}\left({x}\right)=\mathrm{1}+{x}−\mathrm{2}{x}+{x}^{\mathrm{2}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${f}\left({x}\right)=\mathrm{1} \\ $$

Commented by youssoufab last updated on 10/Sep/17

f(x)+xf(1−x)=x+1 ⇔f(x+1/2)+(x+1/2)f(−x−1/2)=x+1/2+1 y=x+1/2 ⇔f(y)+yf(−y)=y+1 ⇔f(y)=y+1−yf(−y) ⇔f(−y)=−y+1+yf(y) ⇔f(y)=y+1−y[−y+1+yf(y)] ⇔f(y)=y+1+y^2 −y−y^2 f(y) ⇔f(y)=1+y^2 −y^2 f(y) ⇔(1+y^2 )f(y)=1+y^2 ⇔f(y)=((1+y^2 )/(1+y^2 )) f(y)=1

$$ \\ $$$${f}\left({x}\right)+{xf}\left(\mathrm{1}−{x}\right)={x}+\mathrm{1} \\ $$$$\Leftrightarrow{f}\left({x}+\mathrm{1}/\mathrm{2}\right)+\left({x}+\mathrm{1}/\mathrm{2}\right){f}\left(−{x}−\mathrm{1}/\mathrm{2}\right)={x}+\mathrm{1}/\mathrm{2}+\mathrm{1} \\ $$$${y}={x}+\mathrm{1}/\mathrm{2} \\ $$$$\Leftrightarrow{f}\left({y}\right)+{yf}\left(−{y}\right)={y}+\mathrm{1} \\ $$$$\Leftrightarrow{f}\left({y}\right)={y}+\mathrm{1}−{yf}\left(−{y}\right) \\ $$$$\Leftrightarrow{f}\left(−{y}\right)=−{y}+\mathrm{1}+{yf}\left({y}\right) \\ $$$$\Leftrightarrow{f}\left({y}\right)={y}+\mathrm{1}−{y}\left[−{y}+\mathrm{1}+{yf}\left({y}\right)\right] \\ $$$$\Leftrightarrow{f}\left({y}\right)={y}+\mathrm{1}+{y}^{\mathrm{2}} −{y}−{y}^{\mathrm{2}} {f}\left({y}\right) \\ $$$$\Leftrightarrow{f}\left({y}\right)=\mathrm{1}+{y}^{\mathrm{2}} −{y}^{\mathrm{2}} {f}\left({y}\right) \\ $$$$\Leftrightarrow\left(\mathrm{1}+{y}^{\mathrm{2}} \right){f}\left({y}\right)=\mathrm{1}+{y}^{\mathrm{2}} \\ $$$$\Leftrightarrow{f}\left({y}\right)=\frac{\mathrm{1}+{y}^{\mathrm{2}} }{\mathrm{1}+{y}^{\mathrm{2}} } \\ $$$${f}\left({y}\right)=\mathrm{1} \\ $$

Commented by $@ty@m last updated on 10/Sep/17