Question Number 87023 by john santu last updated on 02/Apr/20
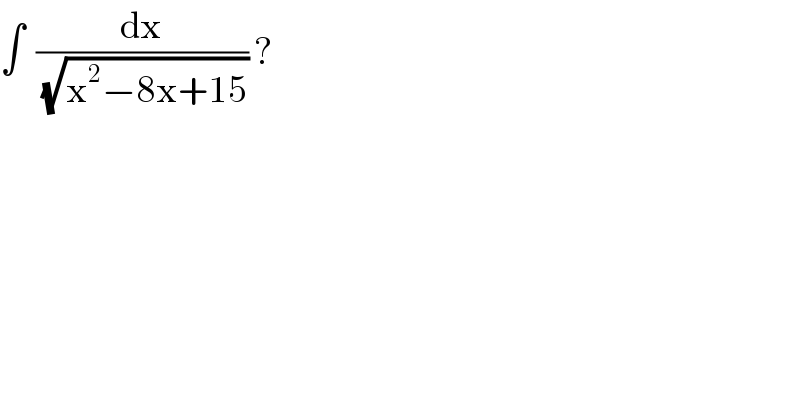
$$\int\:\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{8x}+\mathrm{15}}}\:?\: \\ $$
Commented by john santu last updated on 02/Apr/20
![∫ (dx/( (√((x−4)^2 −1)))) = I [ x−4 = sec t ] ∫ ((sec t tan t dt)/( (√(sec^2 t−1)))) = ∫ sec t dt = ln ∣ sec t + tan t ∣ +c = ln ∣x−4+(√(x^2 −8x+15)) ∣ + c](https://www.tinkutara.com/question/Q87024.png)
$$\int\:\:\frac{{dx}}{\:\sqrt{\left({x}−\mathrm{4}\right)^{\mathrm{2}} −\mathrm{1}}}\:=\:{I} \\ $$$$\left[\:{x}−\mathrm{4}\:=\:\mathrm{sec}\:{t}\:\right]\: \\ $$$$\int\:\:\frac{\mathrm{sec}\:{t}\:\mathrm{tan}\:{t}\:{dt}}{\:\sqrt{\mathrm{sec}\:^{\mathrm{2}} {t}−\mathrm{1}}}\:=\:\int\:\mathrm{sec}\:{t}\:{dt}\: \\ $$$$=\:\mathrm{ln}\:\mid\:\mathrm{sec}\:{t}\:+\:\mathrm{tan}\:{t}\:\mid\:+{c}\: \\ $$$$=\:\mathrm{ln}\:\mid{x}−\mathrm{4}+\sqrt{{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{15}}\:\mid\:+\:{c} \\ $$
