Question Number 87027 by john santu last updated on 02/Apr/20
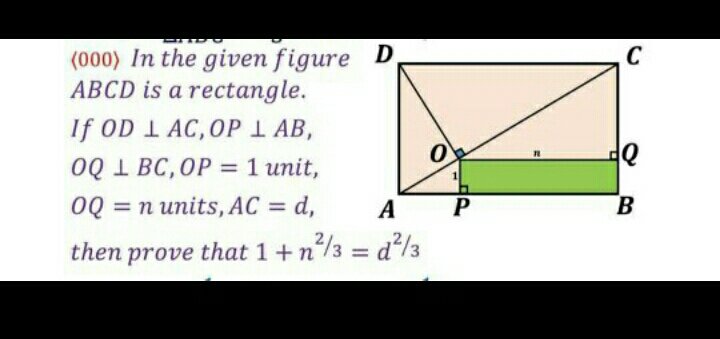
Answered by som(math1967) last updated on 05/Apr/20
![∠DCO=alt∠OAP=θ(let) ∠COQ=∠OAP=θ again ∠ADO=∠DCO=θns [△ADO∼△DCO] OC=nsecθ ,OA=OPcosecθ=cosecθ [∵n=OQ] ∴OC+OA=AC nsecθ+cosecθ=d .......1) nowOD=OCtanθ [from△ODC] OD=nsecθtanθ from△ODA OD=OAcotθ ∴OD=cosecθcotθ nsecθtanθ=cosecθcotθ ntan^2 θ=cotθ tan^3 θ=(1/n) tanθ=((1/n))^(1/3) ∴secθ=(((1+n^(2/3) )^(1/2) )/n^(1/3) ) cosecθ=(((1+n^(2/3) )^(1/2) )/1) from 1) nsecθ+cosecθ=d n.(((1+n^(2/3) )^(1/2) )/n^(1/3) ) +(1+n^(2/3) )^(1/2) =d n^(2/3) (1+n^(2/3) )^(1/2) +(1+n^(2/3) )^(1/2) =d (1+n^(2/3) )^(1/2) (1+n^(2/3) )=d (1+n^(2/3) )^(3/2) =d ∴1+n^(2/3) =d^(2/3)](https://www.tinkutara.com/question/Q87663.png)
$$\angle{DCO}={alt}\angle{OAP}=\theta\left({let}\right) \\ $$$$\angle{COQ}=\angle{OAP}=\theta \\ $$$${again}\:\angle{ADO}=\angle{DCO}=\theta{ns} \\ $$$$\left[\bigtriangleup{ADO}\sim\bigtriangleup{DCO}\right] \\ $$$${OC}={nsec}\theta\:,{OA}={OPcosec}\theta={cosec}\theta \\ $$$$\:\:\:\:\left[\because{n}={OQ}\right] \\ $$$$\therefore{OC}+{OA}={AC} \\ $$$$\left.{nsec}\theta+{cosec}\theta={d}\:\:…….\mathrm{1}\right) \\ $$$${nowOD}={OCtan}\theta\:\:\left[{from}\bigtriangleup{ODC}\right] \\ $$$$\:{OD}={nsec}\theta{tan}\theta \\ $$$${from}\bigtriangleup{ODA}\:\:{OD}={OAcot}\theta \\ $$$$\:\therefore{OD}={cosec}\theta{cot}\theta \\ $$$${nsec}\theta{tan}\theta={cosec}\theta{cot}\theta \\ $$$${ntan}^{\mathrm{2}} \theta={cot}\theta \\ $$$${tan}^{\mathrm{3}} \theta=\frac{\mathrm{1}}{{n}}\:\:{tan}\theta=\left(\frac{\mathrm{1}}{{n}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\therefore{sec}\theta=\frac{\left(\mathrm{1}+{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{n}^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$${cosec}\theta=\frac{\left(\mathrm{1}+{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}} \\ $$$$\left.{from}\:\mathrm{1}\right)\:{nsec}\theta+{cosec}\theta={d} \\ $$$${n}.\frac{\left(\mathrm{1}+{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{n}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:+\left(\mathrm{1}+{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} ={d} \\ $$$${n}^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{1}+{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} +\left(\mathrm{1}+{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} ={d} \\ $$$$\left(\mathrm{1}+{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}+{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)={d} \\ $$$$\left(\mathrm{1}+{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} ={d} \\ $$$$\therefore\mathrm{1}+{n}^{\frac{\mathrm{2}}{\mathrm{3}}} ={d}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$ \\ $$
