Question Number 87550 by jagoll last updated on 05/Apr/20
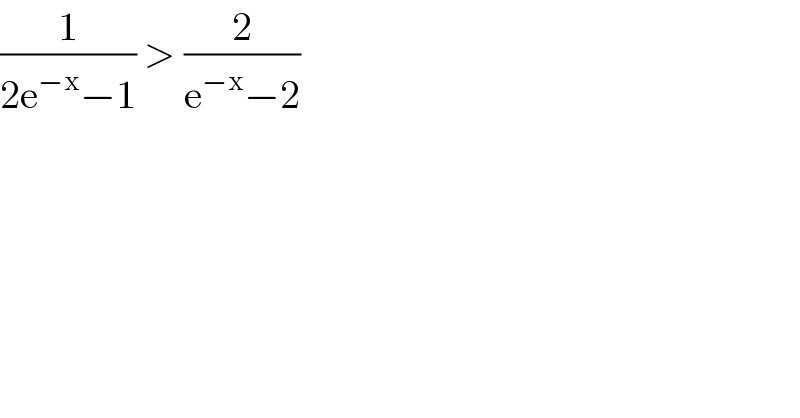
$$\frac{\mathrm{1}}{\mathrm{2e}^{−\mathrm{x}} −\mathrm{1}}\:>\:\frac{\mathrm{2}}{\mathrm{e}^{−\mathrm{x}} −\mathrm{2}} \\ $$
Commented by john santu last updated on 05/Apr/20
![⇒(e^x /(2−e^x )) > ((2e^x )/(1−2e^x )) [ let e^x = t ] (t/(2−t)) > ((2t)/(1−2t)) ⇒ ((t−2t^2 −4t+2t^2 )/((2−t)(1−2t))) > 0 ((−3t)/((2−t)(1−2t))) > 0 ⇒(1/2) < t < 2 e^(ln ((1/2))) < e^x < e^(ln(2)) −ln(2) < x < ln (2)](https://www.tinkutara.com/question/Q87552.png)
$$\Rightarrow\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{2}−\mathrm{e}^{\mathrm{x}} }\:>\:\frac{\mathrm{2e}^{\mathrm{x}} }{\mathrm{1}−\mathrm{2e}^{\mathrm{x}} } \\ $$$$\left[\:\mathrm{let}\:\mathrm{e}^{\mathrm{x}} \:=\:\mathrm{t}\:\right]\: \\ $$$$\frac{\mathrm{t}}{\mathrm{2}−\mathrm{t}}\:>\:\frac{\mathrm{2t}}{\mathrm{1}−\mathrm{2t}}\:\Rightarrow\:\frac{\mathrm{t}−\mathrm{2t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{2t}^{\mathrm{2}} }{\left(\mathrm{2}−\mathrm{t}\right)\left(\mathrm{1}−\mathrm{2t}\right)}\:>\:\mathrm{0} \\ $$$$\frac{−\mathrm{3t}}{\left(\mathrm{2}−\mathrm{t}\right)\left(\mathrm{1}−\mathrm{2t}\right)}\:>\:\mathrm{0}\: \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\:<\:\mathrm{t}\:<\:\mathrm{2}\: \\ $$$$\mathrm{e}^{\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \:<\:\mathrm{e}^{\mathrm{x}} \:<\:\mathrm{e}^{\mathrm{ln}\left(\mathrm{2}\right)} \\ $$$$−\mathrm{ln}\left(\mathrm{2}\right)\:<\:\mathrm{x}\:<\:\mathrm{ln}\:\left(\mathrm{2}\right)\: \\ $$
Commented by jagoll last updated on 05/Apr/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
