Question Number 153108 by peter frank last updated on 04/Sep/21
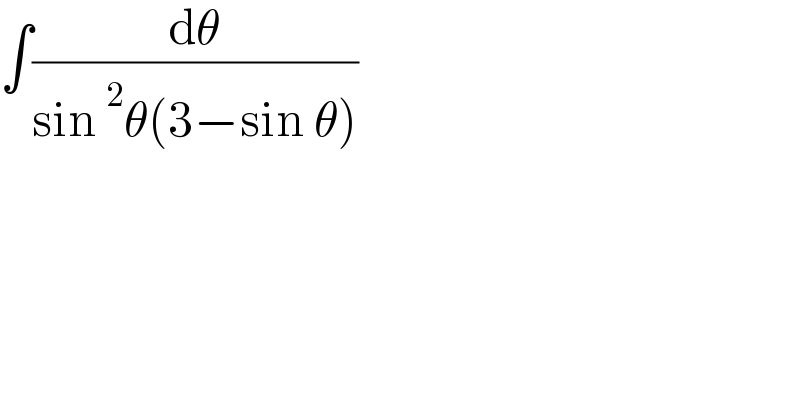
$$\int\frac{\mathrm{d}\theta}{\mathrm{sin}\:^{\mathrm{2}} \theta\left(\mathrm{3}−\mathrm{sin}\:\theta\right)} \\ $$
Answered by MJS_new last updated on 05/Sep/21
![∫(dθ/((3−sin θ)sin^2 θ))= [t=tan (θ/2) → dθ=((2dt)/(t^2 +1))] =(1/2)∫(((t^2 +1)^2 )/(t^2 (3t^2 −2t+3)))dt= =∫((1/6)+(1/(9t))+(1/(6t^2 ))+(2/(9(3t^2 −2t+3))))dt= =(1/6)t+(1/9)ln t −(1/(6t))+((√2)/(18))arctan (((√2)(3t−1))/4) ...](https://www.tinkutara.com/question/Q153142.png)
$$\int\frac{{d}\theta}{\left(\mathrm{3}−\mathrm{sin}\:\theta\right)\mathrm{sin}^{\mathrm{2}} \:\theta}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\:\rightarrow\:{d}\theta=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} \left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{3}\right)}{dt}= \\ $$$$=\int\left(\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{9}{t}}+\frac{\mathrm{1}}{\mathrm{6}{t}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{9}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{3}\right)}\right){dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}{t}+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:{t}\:−\frac{\mathrm{1}}{\mathrm{6}{t}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{18}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}}\left(\mathrm{3}{t}−\mathrm{1}\right)}{\mathrm{4}} \\ $$$$… \\ $$
Commented by peter frank last updated on 05/Sep/21

$$\mathrm{third}\:\mathrm{line}\:\mathrm{to}\:\mathrm{fouth}\:\mathrm{line}\:\mathrm{clarification} \\ $$$$\mathrm{please} \\ $$
