Question Number 133050 by mnjuly1970 last updated on 18/Feb/21
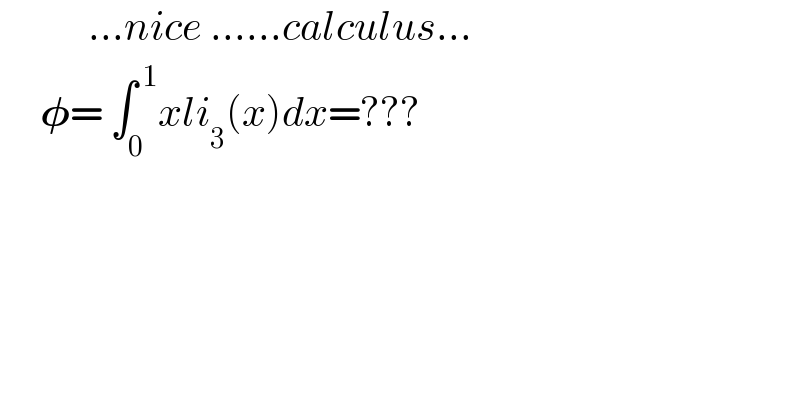
$$\:\:\:\:\:\:\:\:\:\:\:…{nice}\:……{calculus}… \\ $$$$\:\:\:\:\:\boldsymbol{\phi}=\:\int_{\mathrm{0}\:} ^{\:\mathrm{1}} {xli}_{\mathrm{3}} \left({x}\right){dx}=??? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 18/Feb/21
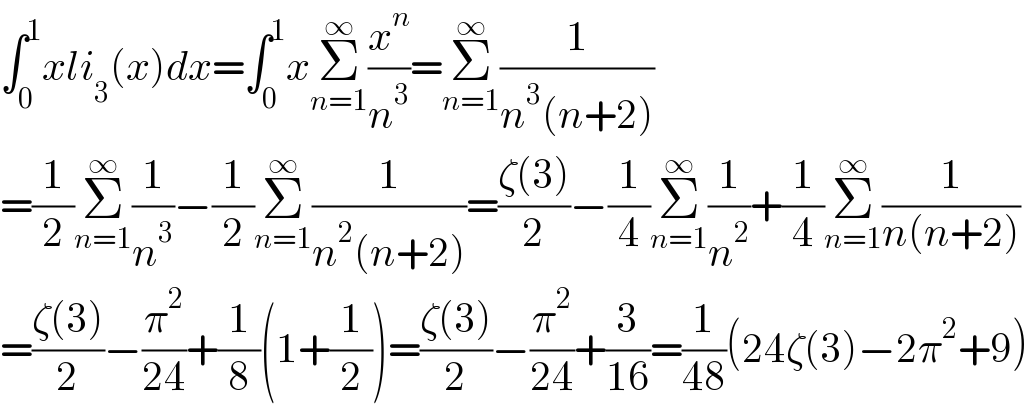
$$\int_{\mathrm{0}} ^{\mathrm{1}} {xli}_{\mathrm{3}} \left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}^{\mathrm{3}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} \left({n}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }β\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{2}\right)}=\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{2}}β\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{2}\right)} \\ $$$$=\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{2}}β\frac{\pi^{\mathrm{2}} }{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{2}}β\frac{\pi^{\mathrm{2}} }{\mathrm{24}}+\frac{\mathrm{3}}{\mathrm{16}}=\frac{\mathrm{1}}{\mathrm{48}}\left(\mathrm{24}\zeta\left(\mathrm{3}\right)β\mathrm{2}\pi^{\mathrm{2}} +\mathrm{9}\right) \\ $$
Commented by mnjuly1970 last updated on 18/Feb/21
$${thank}\:{you}\:{for}\:{your}\:{effort}.. \\ $$$${grateful}… \\ $$
Answered by mnjuly1970 last updated on 18/Feb/21
![π=[(x^2 /2)li_3 (x)]_0 ^1 β(1/2)β«_0 ^( 1) xli_2 (x)dx =(1/2)li_3 (1)β(Ξ¦/2) where Ξ¦=β«_0 ^( 1) xli_2 (x)dx =[(x^2 /2)li_2 (x)]_0 ^1 β(1/2)β«_0 ^( 1) xli_1 (x)dx =(Ο^2 /(12))β(Ξ¨/2) Ξ¨=β«_0 ^( 1) xli_1 (x)dx=Ξ£_(n=1) ^β β«_0 ^( 1) (x^(n+1) /n)dx =Ξ£_(n=1) ^β (1/(n(n+2)))=(1/2)(Ξ£_(n=1) ^β (1/n)β(1/(n+2))) =(1/2)((1/1)β(1/3)+(1/2)β(1/4)+(1/3)β(1/5)+(1/4)β(1/6)+....) =(3/4) β΄ π =((ΞΆ(3))/2) β(1/2)((Ο^2 /(12))β(1/2)((3/4))) =((ΞΆ(3))/2)β(Ο^2 /(24))+(3/(16)) ....](https://www.tinkutara.com/question/Q133084.png)
$$\:\:\:\:\boldsymbol{\phi}=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{li}_{\mathrm{3}} \left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} β\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} {xli}_{\mathrm{2}} \left({x}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}{li}_{\mathrm{3}} \left(\mathrm{1}\right)β\frac{\Phi}{\mathrm{2}} \\ $$$$\:\:\:\:{where}\:\:\Phi=\int_{\mathrm{0}} ^{\:\mathrm{1}} {xli}_{\mathrm{2}} \left({x}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{li}_{\mathrm{2}} \left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} β\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} {xli}_{\mathrm{1}} \left({x}\right){dx} \\ $$$$\:\:\:\:\:\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}β\frac{\Psi}{\mathrm{2}} \\ $$$$\:\:\:\:\Psi=\int_{\mathrm{0}} ^{\:\mathrm{1}} {xli}_{\mathrm{1}} \left({x}\right){dx}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{n}+\mathrm{1}} }{{n}}{dx} \\ $$$$\:\:\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}β\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}}β\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}β\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}}β\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{4}}β\frac{\mathrm{1}}{\mathrm{6}}+….\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\:\:\:\therefore\:\:\:\boldsymbol{\phi}\:=\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{2}}\:β\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{12}}β\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{2}}β\frac{\pi^{\mathrm{2}} }{\mathrm{24}}+\frac{\mathrm{3}}{\mathrm{16}}\:…. \\ $$
Commented by Dwaipayan Shikari last updated on 18/Feb/21
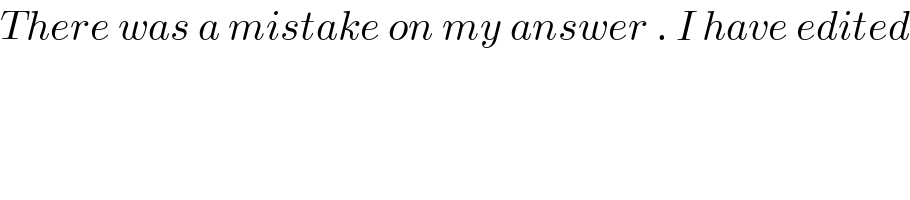
$${There}\:{was}\:{a}\:{mistake}\:{on}\:{my}\:{answer}\:.\:{I}\:{have}\:{edited} \\ $$
Commented by mnjuly1970 last updated on 18/Feb/21
$$\:\:{grateful}\:{sir}\:{payan}… \\ $$$$ \\ $$