Question Number 87995 by abdomathmax last updated on 07/Apr/20
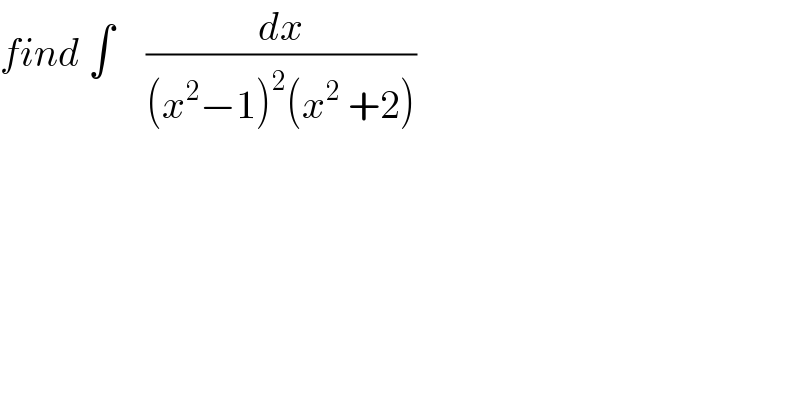
$${find}\:\int\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} \:+\mathrm{2}\right)} \\ $$
Answered by redmiiuser last updated on 08/Apr/20
![(1/(x^2 −1))=t (dx/((x^2 −1)^(2 ) ))=−dt x^2 +2=(1/t)+3=((1+3t)/t) ∫((−t.dt)/(1+3t)) 1+3t=z 3.dt=dz ((−1)/3)∫(((z−1).dz)/(3.z)) =((−1)/9)[∫dz−∫(dz/z)] =((−1)/9)[z−lnz]+c =(1/9)[ln z−z]+c =(1/9)[ln (((x^2 +2)/(x^2 −1)))−((x^2 +2)/(x^2 −1))]+c](https://www.tinkutara.com/question/Q88051.png)
$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}={t} \\ $$$$\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}\:} \:}=−{dt} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}=\frac{\mathrm{1}}{{t}}+\mathrm{3}=\frac{\mathrm{1}+\mathrm{3}{t}}{{t}} \\ $$$$\int\frac{−{t}.{dt}}{\mathrm{1}+\mathrm{3}{t}} \\ $$$$\mathrm{1}+\mathrm{3}{t}={z} \\ $$$$\mathrm{3}.{dt}={dz} \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}}\int\frac{\left({z}−\mathrm{1}\right).{dz}}{\mathrm{3}.{z}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{9}}\left[\int{dz}−\int\frac{{dz}}{{z}}\right] \\ $$$$=\frac{−\mathrm{1}}{\mathrm{9}}\left[{z}−{lnz}\right]+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left[\mathrm{ln}\:{z}−{z}\right]+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left[\mathrm{ln}\:\left(\frac{{x}^{\mathrm{2}} +\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}\right)−\frac{{x}^{\mathrm{2}} +\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}\right]+{c} \\ $$
